
【題目】如圖,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分別是AC、BC中點. 
(1)求證:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值.
【答案】
(1)證明:∵F、G分別是AC、BC中點.
∴FG∥AB,
∵FG平面ABE,AB平面ABE,
∴FG∥平面ABE,
∵DE∥BC,BC=2DE,G是BC中點,
∴DE ![]() BG,∴四邊形DEBG是平行四邊形,
BG,∴四邊形DEBG是平行四邊形,
∴DG∥BE,
∵DG平面ABE,BE平面ABE,
∴DG∥平面ABE,
∵DG∩FG=G,DG,FG平面DFG,
AB∩BE=B,AB,BE平面ABE,
∴平面DFG∥平面ABE
(2)解:∵DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分別是AC、BC中點.
∴以C為原點,CA為x軸,以CB為y軸,以CD為z軸,建立空間直角坐標系,
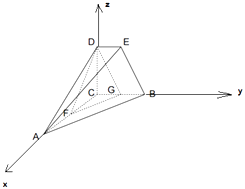
∵AC=2BC=2CD=4,
∴A(4,0,0),B(0,2,0),C(0,0,2),E(0,1,2),
![]() =(﹣4,1,2),
=(﹣4,1,2), ![]() =(﹣4,2,0),
=(﹣4,2,0), ![]() =(﹣4,0,2),
=(﹣4,0,2),
設平面ABE的法向量 ![]() =(x,y,z),
=(x,y,z),
則 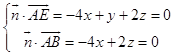 ,取x=1,得
,取x=1,得 ![]() =(1,0,2),
=(1,0,2),
平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
則cos< ![]() >=
>= ![]() .
.
∴二面角E﹣AB﹣C的余弦值為cosα= ![]() ,
,
則sinα= ![]() ,tanα=
,tanα= ![]() =
= ![]() .
.
∴二面角E﹣AB﹣C的正切值為 ![]() .
.
【解析】(1)推導出FG∥AB,從而FG∥平面ABE,從而出四邊形DEBG是平行四邊形,從而DG∥BE,進而DG∥平面ABE,由此能證明平面DFG∥平面ABE.(2)以C為原點,CA為x軸,以CB為y軸,以CD為z軸,建立空間直角坐標系,利用向量法能求出二面角E﹣AB﹣C的正切值.


科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形, 且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1
,AB=2,PA=1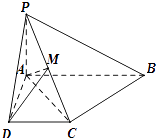
(1)求證:AB∥平面PCD;
(2)求證:BC⊥平面PAC;
(3)若M是PC的中點,求三棱錐C﹣MAD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形ABCD是平行四邊形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB= ![]() ,EF=1,BC=
,EF=1,BC= ![]() ,且M是BD的中點..
,且M是BD的中點.. 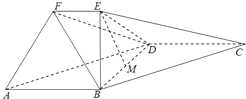
(1)求證:EM∥平面ADF;
(2)求直線DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國詩詞大會》(第二季)亮點頗多,十場比賽每場都有一首特別設計的開場詩詞,在聲光舞美的配合下,百人團齊聲朗誦,別有韻味.若《將進酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另確定的兩首詩詞排在后六場,且《將進酒》排在《望岳》的前面,《山居秋暝》與《送杜少府之任蜀州》不相鄰且均不排在最后,則后六場的排法有( )
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com