
【題目】在平面直角坐標系中,圓C的方程為 ![]() (θ為參數(shù)),以坐標原點O為極點,x軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的單位長度,直線l的極坐標方程為ρcosθ+ρsinθ=m(m∈R).
(θ為參數(shù)),以坐標原點O為極點,x軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的單位長度,直線l的極坐標方程為ρcosθ+ρsinθ=m(m∈R).
(I)當m=3時,判斷直線l與C的位置關(guān)系;
(Ⅱ)當C上有且只有一點到直線l的距離等于 ![]() 時,求C上到直線l距離為2
時,求C上到直線l距離為2 ![]() 的點的坐標.
的點的坐標.
【答案】解:(I)圓C的普通方程為(x﹣1)2+(y﹣1)2=2, ∴圓心坐標為(1,1),半徑r= ![]() .
.
m=3時,直線l的直角坐標方程為x+y﹣3=0.
∴圓心C到直線l的距離d= ![]() =
= ![]() <r.
<r.
∴直線l與圓C相交.
(II)直線l的普通方程為x+y﹣m=0.
∵C上有且只有一點到直線l的距離等于 ![]() ,
,
∴直線l與圓C相離,且圓心到直線的距離為 ![]() .
.
∴圓C上到直線l的距離等于2 ![]() 的點在過圓心C(1,1)且與直線l平行的直線上.
的點在過圓心C(1,1)且與直線l平行的直線上.
∴過圓心C(1,1)且與直線l平行的直線的參數(shù)方程為:  (t為參數(shù)).
(t為參數(shù)).
將:  (t為參數(shù))代入圓C的普通方程得t2=2,
(t為參數(shù))代入圓C的普通方程得t2=2,
∴t1= ![]() ,t2=﹣
,t2=﹣ ![]() .
.
當t= ![]() 時,
時, ![]() ,當t=﹣
,當t=﹣ ![]() 時,
時, ![]() .
.
∴C上到直線l距離為2 ![]() 的點的坐標為(0,2),(2,0)
的點的坐標為(0,2),(2,0)
【解析】(I)將曲線方程化成直角坐標方程,計算圓心到直線的距離與圓的半徑比較大小得出結(jié)論;(II)由題意可知直線與圓相離,且圓心到直線l的距離為2 ![]() ,故到直線l的距離等于2
,故到直線l的距離等于2 ![]() 的點在過圓心且與直線l平行的直線上,求出此直線的參數(shù)方程代入圓的方程求出該點對應的參數(shù),得出該點的坐標.
的點在過圓心且與直線l平行的直線上,求出此直線的參數(shù)方程代入圓的方程求出該點對應的參數(shù),得出該點的坐標.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列 {an} 的前 n 項和為Sn , S1=6,S2=4,Sn>0且S2n , S2n﹣1 , S2n+2成等比數(shù)列,S2n﹣1 , S2n+2 , S2n+1成等差數(shù)列,則a2016等于( )
A.﹣1009
B.﹣1008
C.﹣1007
D.﹣1006
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù) ![]() ,為了得到函數(shù)g(x)=sin2x的圖象,則只需將f(x)的圖象( )
,為了得到函數(shù)g(x)=sin2x的圖象,則只需將f(x)的圖象( )
A.向右平移 ![]() 個長度單位
個長度單位
B.向右平移 ![]() 個長度單位
個長度單位
C.向左平移 ![]() 個長度單位
個長度單位
D.向左平移 ![]() 個長度單位
個長度單位
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)甲、乙兩人每次射擊命中目標的概率分別為 ![]() ,且各次射擊相互獨立,若按甲、乙、甲、乙…的次序輪流射擊,直到有一人擊中目標就停止射擊,則停止射擊時,甲射擊了兩次的概率是( )
,且各次射擊相互獨立,若按甲、乙、甲、乙…的次序輪流射擊,直到有一人擊中目標就停止射擊,則停止射擊時,甲射擊了兩次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() sin2x﹣2cos2x﹣1,x∈R.
sin2x﹣2cos2x﹣1,x∈R.
(Ⅰ)求函數(shù)f(x)的最小正周期和最小值;
(Ⅱ)在△ABC中,A,B,C的對邊分別為a,b,c,已知c= ![]() ,f(C)=0,sinB=2sinA,求a,b的值.
,f(C)=0,sinB=2sinA,求a,b的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知向量 ![]() ,函數(shù)
,函數(shù) ![]() . (Ⅰ)求函數(shù)f(x)的單調(diào)遞增區(qū)間;
. (Ⅰ)求函數(shù)f(x)的單調(diào)遞增區(qū)間;
(Ⅱ)在△ABC中,a,b,c分別為△ABC三個內(nèi)角A,B,C的對邊,若 ![]() ,a=2,求b+c的取值范圍.
,a=2,求b+c的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某工廠生產(chǎn)某種產(chǎn)品的產(chǎn)量x(噸)與相應的生產(chǎn)成本y(萬元)有如下幾組樣本數(shù)據(jù):
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3.1 | 3.9 | 4.5 |
據(jù)相關(guān)性檢驗,這組樣本數(shù)據(jù)具有線性相關(guān)關(guān)系,通過線性回歸分析,求得到其回歸直線的斜率為0.8,則當該產(chǎn)品的生產(chǎn)成本是6.7萬元時,其相應的產(chǎn)量約是( )
A.8
B.8.5
C.9
D.9.5
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù) 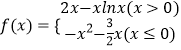 有且僅有四個不同的點關(guān)于直線y=1的對稱點在直線kx+y﹣1=0上,則實數(shù)k的取值范圍為( )
有且僅有四個不同的點關(guān)于直線y=1的對稱點在直線kx+y﹣1=0上,則實數(shù)k的取值范圍為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某地要建造一個邊長為2(單位:km)的正方形市民休閑公園OABC,將其中的區(qū)域ODC開挖成一個池塘,如圖建立平面直角坐標系后,點D的坐標為(1,2),曲線OD是函數(shù)y=ax2圖象的一部分,對邊OA上一點M在區(qū)域OABD內(nèi)作一次函數(shù)y=kx+b(k>0)的圖象,與線段DB交于點N(點N不與點D重合),且線段MN與曲線OD有且只有一個公共點P,四邊形MABN為綠化風景區(qū): 
(1)求證:b=﹣ ![]() ;
;
(2)設(shè)點P的橫坐標為t,①用t表示M、N兩點坐標;②將四邊形MABN的面積S表示成關(guān)于t的函數(shù)S=S(t),并求S的最大值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com