【題目】已知數列 {an} 的前 n 項和為Sn ， S1=6，S2=4，Sn＞0且S2n ， S2n﹣1 ， S2n+2成等比數列，S2n﹣1 ， S2n+2 ， S2n+1成等差數列，則a2016等于（ ）
A.﹣1009
B.﹣1008
C.﹣1007
D.﹣1006
【答案】A
【解析】解：∵數列{an}的前n項和為Sn ， S1=6，S2=4，Sn＞0，且S2n ， S 2n﹣1 ． S 2n+2成等比數列， S2n﹣1 ． S2n+2 ， S2n+1成等差數列，
∴依題意，得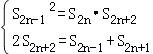 
，
∵Sn＞0，∴2S2n+2= 
+ 
，
即2 
= 
+ 
，
故數列{ }是等差數列，
由S1=6，S2=4，可得S3=12，S4=9，
∴數列{ }是首項為2，公差為1的等差數列．
∴ =2+（n﹣1）=n+1，即S2n=（n+1）2 ，
故S2n﹣1= =（n+1）（n+2），
故S2016=10092 ，
S2015=1009×1010，
故a2016=S2016﹣S2015=﹣1009．
故選：A．
科目：高中數學 來源： 題型：
【題目】在等差數列{an}中，a1=3，其前n項和為Sn ， 等比數列{bn}的各項均為正數，b1=1，公比為q，且b2+S2=12，q= 
（Ⅰ）求an與bn；
（Ⅱ）設數列{cn}滿足cn= 
，求{cn}的前n項和Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線E：y2=2px（p＞0）的焦點為F，過F且垂直于x軸的直線與拋物線E交于A，B兩點，E的準線與x軸交于點C，△CAB的面積為4，以點D（3，0）為圓心的圓D過點A，B． （Ⅰ）求拋物線E和圓D的方程；
（Ⅱ）若斜率為k（|k|≥1）的直線m與圓D相切，且與拋物線E交于M，N兩點，求 
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=|x+m|+|2x﹣1|（m∈R） （I）當m=﹣1時，求不等式f（x）≤2的解集；
（II）設關于x的不等式f（x）≤|2x+1|的解集為A，且[ 
，2]A，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】四棱錐P﹣ABCD的三視圖如圖所示，其五個頂點都在同一球面上，若四棱錐P﹣ABCD的側面積等于4（1+ 
），則該外接球的表面積是（ ） 
A.4π
B.12π
C.24π
D.36π
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校為了解該校高三年級學生數學科學習情況，對廣一模考試數學成績進行分析，從中抽取了n 名學生的成績作為樣本進行統計（該校全體學生的成績均在[60，140），按照[60，70），[70，80），[80，90），[90，100），[100，110），[110，120），[120，130），[130，140）的分組作出頻率分布直方圖如圖1所示，樣本中分數在[70，90）內的所有數據的莖葉圖如圖2所示． 
根據上級統計劃出預錄分數線，有下列分數與可能被錄取院校層次對照表為表（ c ）．
分數 | [50，85] | [85，110] | [110，150] |
可能被錄取院校層次 | 專科 | 本科 | 重本 |
（1）求n和頻率分布直方圖中的x，y的值；
（2）根據樣本估計總體的思想，以事件發生的頻率作為概率，若在該校高三年級學生中任取3 人，求至少有一人是可能錄取為重本層次院校的概率；
（3）在選取的樣本中，從可能錄取為重本和專科兩個層次的學生中隨機抽取3 名學生進行調研，用ξ表示所抽取的3 名學生中為重本的人數，求隨機變量ξ的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△ABC中，AB=AC，D為△ABC外接圓劣弧 
上的點（不與點A，C重合），延長BD至E，延長AD交BC的延長線于F. 
（1）求證：∠CDF=∠EDF；
（2）求證：ABACDF=ADFCFB．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，圓C的方程為 
（θ為參數），以坐標原點O為極點，x軸的正半軸為極軸，建立極坐標系，兩種坐標系中取相同的單位長度，直線l的極坐標方程為ρcosθ+ρsinθ=m（m∈R）．
（I）當m=3時，判斷直線l與C的位置關系；
（Ⅱ）當C上有且只有一點到直線l的距離等于 
時，求C上到直線l距離為2 的點的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
