
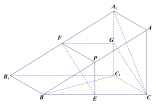
【題目】如圖,三棱柱![]() 的側(cè)面
的側(cè)面![]() 是平行四邊形,
是平行四邊形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分別是
分別是![]() 的中點.
的中點.

(Ⅰ)求證:![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(Ⅰ)詳見解析;(Ⅱ)詳見解析;(Ⅲ)當(dāng)點![]() 是線段
是線段![]() 的中點時,
的中點時,![]() 平面
平面![]() .此時,
.此時,![]()
【解析】
(Ⅰ)由![]() ,利用面面垂直的性質(zhì),證得
,利用面面垂直的性質(zhì),證得![]() 平面
平面![]() ,在線面垂直的性質(zhì),即可得到
,在線面垂直的性質(zhì),即可得到![]() .
.
(Ⅱ)取![]() 中點
中點![]() ,連
,連![]() 連
連![]() ,得到四邊形
,得到四邊形![]() 為平行四邊形,又由
為平行四邊形,又由![]() 是
是![]() 的中點,證得
的中點,證得![]() ,且
,且![]() ,進而得到
,進而得到![]() ,利用線面平行的判定定理,即可證得
,利用線面平行的判定定理,即可證得![]() 平面
平面![]() .
.
(Ⅲ)取![]() 的中點
的中點![]() ,連
,連![]() ,連
,連![]() ,由線面垂直的性質(zhì),得到
,由線面垂直的性質(zhì),得到![]()
![]() ,
,![]()
![]() ,又在在△
,又在在△![]() 中,利用中位線得
中,利用中位線得![]() ,再由(Ⅱ)知
,再由(Ⅱ)知![]() ,進而得到
,進而得到![]() 平面
平面![]() ,得出結(jié)論.
,得出結(jié)論.
(Ⅰ)因為![]() ,又平面
,又平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因為![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)取![]() 中點
中點![]() ,連
,連![]() 連
連![]() .
.
在△![]() 中,因為
中,因為![]() 分別是
分別是![]() 中點,
中點,
所以![]() ,且
,且![]() .
.
在平行四邊形![]() 中,因為
中,因為![]() 是
是![]() 的中點,
的中點,
所以![]() ,且
,且![]() .
.
所以![]() ,且
,且![]() .
.
所以四邊形![]() 是平行四邊形.
是平行四邊形.
所以![]() .
.
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅲ)在線段![]() 上存在點
上存在點![]() ,使得
,使得![]() 平面
平面![]() .
.
取![]() 的中點
的中點![]() ,連
,連![]() ,連
,連![]() .
.
因為![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,
所以![]()
![]() ,
,![]()
![]() .
.
在△![]() 中,因為
中,因為![]() 分別是
分別是![]() 中點,所以
中點,所以![]() .
.
又由(Ⅱ)知![]() ,
,
所以![]()
![]() ,
,![]() .
.
由![]()
![]() 得
得![]() 平面
平面![]() .
.
故當(dāng)點![]() 是線段
是線段![]() 的中點時,
的中點時,![]() 平面
平面![]() .此時,
.此時,![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,一輛汽車從![]() 市出發(fā)沿海岸一條直公路以
市出發(fā)沿海岸一條直公路以![]() 的速度向東勻速行駛,汽車開動時,在
的速度向東勻速行駛,汽車開動時,在![]() 市南偏東方向距
市南偏東方向距![]() 市
市![]() 且與海岸距離為
且與海岸距離為![]() 的海上
的海上![]() 處有一快艇與汽車同時出發(fā),要把一份稿件送給這輛汽車的司機.
處有一快艇與汽車同時出發(fā),要把一份稿件送給這輛汽車的司機.

(1)快艇至少以多大的速度行駛才能把稿件送到司機手中?
(2)在(1)的條件下,求快艇以最小速度行駛時的行駛方向與![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某同學(xué)大學(xué)畢業(yè)后,決定利用所學(xué)專業(yè)進行自主創(chuàng)業(yè),經(jīng)過市場調(diào)查,生產(chǎn)一小型電子產(chǎn)品需投入固定成本2萬元,每生產(chǎn)![]() 萬件,需另投入流動成本
萬件,需另投入流動成本![]() 萬元,當(dāng)年產(chǎn)量小于
萬元,當(dāng)年產(chǎn)量小于![]() 萬件時,
萬件時,![]() (萬元);當(dāng)年產(chǎn)量不小于7萬件時,
(萬元);當(dāng)年產(chǎn)量不小于7萬件時,![]() (萬元).已知每件產(chǎn)品售價為6元,假若該同學(xué)生產(chǎn)的商品當(dāng)年能全部售完.
(萬元).已知每件產(chǎn)品售價為6元,假若該同學(xué)生產(chǎn)的商品當(dāng)年能全部售完.
(1)寫出年利潤![]() (萬年)關(guān)于年產(chǎn)量
(萬年)關(guān)于年產(chǎn)量![]() (萬件)的函數(shù)解析式;(注:年利潤=年銷售收入-固定成本-流動成本)
(萬件)的函數(shù)解析式;(注:年利潤=年銷售收入-固定成本-流動成本)
(2)當(dāng)年產(chǎn)量約為多少萬件時,該同學(xué)的這一產(chǎn)品所獲年利潤最大?最大年利潤是多少?
(取![]() ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高三年級學(xué)生為了慶祝教師節(jié),同學(xué)們?yōu)槔蠋熤谱髁艘淮笈环N規(guī)格的手工藝品,這種工藝品有![]()
![]() 兩項技術(shù)指標(biāo)需要檢測,設(shè)各項技術(shù)指標(biāo)達標(biāo)與否互不影響,若
兩項技術(shù)指標(biāo)需要檢測,設(shè)各項技術(shù)指標(biāo)達標(biāo)與否互不影響,若![]() 項技術(shù)指標(biāo)達標(biāo)的概率為
項技術(shù)指標(biāo)達標(biāo)的概率為![]() 項技術(shù)指標(biāo)達標(biāo)的概率為
項技術(shù)指標(biāo)達標(biāo)的概率為![]() ,按質(zhì)量檢驗規(guī)定:兩項技術(shù)指標(biāo)都達標(biāo)的工藝品為合格品.
,按質(zhì)量檢驗規(guī)定:兩項技術(shù)指標(biāo)都達標(biāo)的工藝品為合格品.
(1)求一個工藝品經(jīng)過檢測至少一項技術(shù)指標(biāo)達標(biāo)的概率;
(2)任意依次抽取該工藝品4個,設(shè)![]() 表示其中合格品的個數(shù),求
表示其中合格品的個數(shù),求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,a,b,c分別為內(nèi)角A,B,C的對邊,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面積S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,由一塊扇形空地![]() ,其中
,其中![]() ,
,![]() 米,計劃在此扇形空地區(qū)域為學(xué)生建燈光籃球運動場,
米,計劃在此扇形空地區(qū)域為學(xué)生建燈光籃球運動場,![]() 區(qū)域內(nèi)安裝一批照明燈,點
區(qū)域內(nèi)安裝一批照明燈,點![]() 、
、![]() 選在線段
選在線段![]() 上(點
上(點![]() 、
、![]() 分別不與點
分別不與點![]() 、
、![]() 重合),且
重合),且![]() .
.

(1)若![]() 點在距離
點在距離![]() 點
點![]() 米處,求點
米處,求點![]() 、
、![]() 之間的距離;
之間的距離;
(2)為了使運動場地區(qū)域最大化,要求![]() 面積盡可能的小,記
面積盡可能的小,記![]() ,請用
,請用![]() 表示
表示![]() 的面積
的面積![]() ,并求
,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的最小正周期為
的最小正周期為![]() ,將函數(shù)
,將函數(shù)![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度,再向下平移
個單位長度,再向下平移![]() 個單位長度,得到函數(shù)
個單位長度,得到函數(shù)![]() 的圖像.
的圖像.
(1)求函數(shù)![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)在銳角![]() 中,角
中,角![]() 的對邊分別為
的對邊分別為![]() ,若
,若![]() ,
,![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]()
(1)若函數(shù)![]() 的圖象與函數(shù)
的圖象與函數(shù)![]() 的圖象相切,求
的圖象相切,求![]() 的值;
的值;
(2)設(shè)函數(shù)![]() ,
,![]() . 若存在
. 若存在![]() ,
,![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com