
【題目】2017年“雙節”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速![]() 分成六段:
分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如圖的頻率分布直方圖.
后得到如圖的頻率分布直方圖.
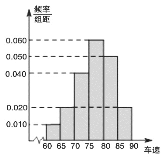
(1)調查公司在采樣中,用到的是什么抽樣方法?
(2)求這40輛小型車輛車速的眾數、中位數及平均數的估計值;
(3)若從車速在![]() 的車輛中任抽取2輛,求車速在
的車輛中任抽取2輛,求車速在![]() 的車輛至少有一輛的概率.
的車輛至少有一輛的概率.
【答案】(1)系統抽樣;(2)見解析;(3)![]()
【解析】
(1)這個抽樣是按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,是一個具有相同間隔的抽樣,并且總體的個數比較多,這是一個系統抽樣;
(2)選出直方圖中最高的矩形求出其底邊的中點即為眾數;求出從左邊開始小矩形的面積和為0.5對應的橫軸的左邊即為中位數;利用各個小矩形的面積乘以對應矩形的底邊的中點的和為數據的平均數;
(3)從圖中可知,車速在[60,65)的車輛數和車速在[65,70)的車輛數.從車速在(60,70)的車輛中任抽取2輛,設車速在[60,65)的車輛設為a,b,車速在[65,70)的車輛設為c,d,e,f,列出各自的基本事件數,從而求出相應的概率即可.
(1)系統抽樣.
(2)眾數的估計值為最高的矩形的中點,即![]()
設圖中虛線所對應的車速為![]() ,則中位數的估計值為:
,則中位數的估計值為:
![]() ,
,
解得![]()
即中位數的估計值為![]() .
.
平均數的估計值為:![]() ,
,
(3)車速在![]() 的車輛數為:2
的車輛數為:2
車速在![]() 的車輛數為:4
的車輛數為:4
設車速在![]() 的車輛為
的車輛為![]() ,車速在
,車速在![]() 的車輛為
的車輛為![]() ,
,
則基本事件有:
![]() ,
,
![]() ,
,
共15種,其中,車速在![]() 的車輛至少有一輛的事件有:
的車輛至少有一輛的事件有:
![]() ,
,
![]() 共14種,
共14種,
所以車速在![]() 的車輛至少有一輛的概率為
的車輛至少有一輛的概率為![]()


科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD的底面ABCD是平行四邊形,BA=BD=![]() ,AD=2,PA=PD=
,AD=2,PA=PD=![]() ,E,F分別是棱AD,PC的中點.
,E,F分別是棱AD,PC的中點.

(1)證明:EF∥平面PAB;
(2)若二面角P-AD-B為60°.
①證明:平面PBC⊥平面ABCD;
②求直線EF與平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點.
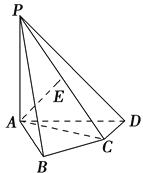
(1)證明:AE⊥平面PCD;
(2)求二面角A-PD-C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某區“創文明城區”(簡稱“創城”)活動中,教委對本區![]() 四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
學校 |
|
|
|
|
抽查人數 | 50 | 15 | 10 | 25 |
“創城”活動中參與的人數 | 40 | 10 | 9 | 15 |
(注:參與率是指:一所學校“創城”活動中參與的人數與被抽查人數的比值)假設每名高中學生是否參與”創城”活動是相互獨立的.
(1)若該區共2000名高中學生,估計![]() 學校參與“創城”活動的人數;
學校參與“創城”活動的人數;
(2)在隨機抽查的100名高中學生中,隨機抽取1名學生,求恰好該生沒有參與“創城”活動的概率;
(3)在上表中從![]() 兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好
兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好![]() 兩校各有1人沒有參與“創城”活動的概率是多少?
兩校各有1人沒有參與“創城”活動的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() 是等邊三角形,
是等邊三角形, ![]() 為
為![]() 的中點,四邊形
的中點,四邊形![]() 為直角梯形,
為直角梯形, ![]()
![]()
![]()
![]() .
.
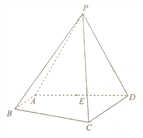
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求四棱錐![]() 的體積;
的體積;
(3)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,游客從某旅游景區的景點A處下山至C處有兩種路徑.一種是從A沿直線步行到C,另一種是先從A沿索道乘纜車到B,然后從B沿直線步行到C.現有甲、乙兩位游客從A處下山,甲沿AC勻速步行,速度為![]() .在甲出發
.在甲出發![]() 后,乙從A乘纜車到B,在B處停留
后,乙從A乘纜車到B,在B處停留![]() 后,再從B勻速步行到C.假設纜車勻速直線運動的速度為
后,再從B勻速步行到C.假設纜車勻速直線運動的速度為![]() ,山路AC長為
,山路AC長為![]() ,經測量,
,經測量,![]() ,
,![]() .當乙出發________分鐘時,乙在纜車上與甲的距離最短.
.當乙出發________分鐘時,乙在纜車上與甲的距離最短.
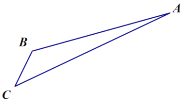
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() :
:![]() 和二次函數
和二次函數![]() ,若直線
,若直線![]() 與二次函數
與二次函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點.
兩點.
(1)求直線![]() 在
在![]() 軸上的截距
軸上的截距![]() ;
;
(2)若點![]() 的坐標為
的坐標為![]() ,求
,求![]() 點的坐標;
點的坐標;
(3)當![]() 時,是否存在直線
時,是否存在直線![]() 與圓
與圓![]() :
:![]() 相切?若存在,求線段
相切?若存在,求線段![]() 的長;若不存在,說明理由.
的長;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com