
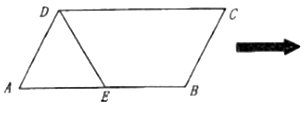
【題目】已知平行四邊形![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點,且△
的中點,且△![]() 是等邊三角形,沿
是等邊三角形,沿![]() 把△
把△![]() 折起至
折起至![]() 的位置,使得
的位置,使得![]() .
.
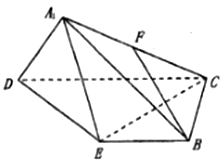
(1)![]() 是線段
是線段![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)求證:![]() ;
;
(3)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)證明見解析;(2)證明見解析;(3)![]() .
.
【解析】
試題分析:(1)取![]() 的中點
的中點![]() ,連結
,連結![]() 、
、![]() ,可證
,可證![]() ,且
,且![]() ,結合條件可得四邊形
,結合條件可得四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,由線面平行的判定定理即可得到
,由線面平行的判定定理即可得到![]() 平面
平面![]() ;(2)由折疊前圖形可得
;(2)由折疊前圖形可得![]() ,在四棱錐
,在四棱錐![]() 中,即有
中,即有![]() ,由余弦定理和勾股定理可得
,由余弦定理和勾股定理可得![]() ,從而證得
,從而證得![]() 平面
平面![]() ,由線面垂直的性質可證得結論;(3)設點
,由線面垂直的性質可證得結論;(3)設點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,進行定體積變換
,進行定體積變換![]() 即可求得點
即可求得點![]() 到平面
到平面![]() 的距離.
的距離.
試題解析:證明:(1)取![]() 的中點
的中點![]() ,連結
,連結![]() 、
、![]() ,
,
因為![]() 為
為![]() 的中點,故
的中點,故![]() ,且
,且![]() ,
,
又![]() ,且
,且![]()
所以四邊形![]() 為平行四邊形,
為平行四邊形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(2)折疊前,![]() ,
,![]() ,即
,即![]() ,
,
在四棱錐![]() 中,即有
中,即有![]() ,
,
在△![]() 中,
中,![]() ,
,![]() ,由余弦定理得
,由余弦定理得![]() ,
,
又![]() ,
,![]() ,由勾股定理的逆定理,得
,由勾股定理的逆定理,得![]() ,
,![]() ,
,
又![]() ,從而
,從而![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,得
,得![]() .
.
(3)由(2)知,![]() 平面
平面![]() ,
,
設點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,則由
,則由![]() ,
,
得![]() ,
,![]() ,
,
解得![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某校高一(1)班有男同學45名,女同學15名,老師按照分層抽樣的方法抽取4人組建了一個課外興趣小組.
(I)求課外興趣小組中男、女同學的人數;
(II)經過一個月的學習、討論,這個興趣小組決定選出兩名同學做某項實驗,方法是從小組里選出一名同學做實驗,該同學做完后,再從小組內剩下的同學中選出一名同學做實驗,求選出的兩名同學中恰有一名女同學的概率;
(III)在(II)的條件下,第一次做實驗的同學A得到的實驗數據為38,40,41,42,44,第二次做實驗的同學B得到的實驗數據為39,40,40,42,44,請問哪位同學的實驗更穩定?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量a=(cos α,sin α),b=(cos β,sin β),c=(-1,0).
(1) 求向量b+c的模的最大值;
(2) 若α=![]() ,且a⊥(b+c),求cos β的值.
,且a⊥(b+c),求cos β的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(ax2-x+1)(a>0,a≠1).
(1) 若a=![]() ,求函數f(x)的值域.
,求函數f(x)的值域.
(2) 當f(x)在區間![]() 上為增函數時,求a的取值范圍.
上為增函數時,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖:某污水處理廠要在一個矩形污水處理池(![]() )的池底水平鋪設污水凈化管道(
)的池底水平鋪設污水凈化管道(![]() 是直角頂點)來處理污水,管道越長污水凈化效果越好,設計要求管道的的接口
是直角頂點)來處理污水,管道越長污水凈化效果越好,設計要求管道的的接口![]() 是
是![]() 的中點,
的中點,![]() 分別落在線段
分別落在線段![]() 上。已知
上。已知![]() 米,
米,![]() 米,記
米,記![]() .
.
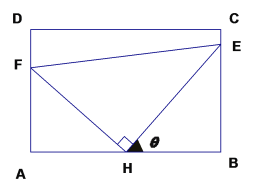
(1)試將污水凈化管道的長度![]() 表示為
表示為![]() 的函數,并寫出定義域;
的函數,并寫出定義域;
(2)若![]() ,求此時管道的長度
,求此時管道的長度![]() ;
;
(3)當![]() 取何值時,污水凈化效果最好?并求出此時管道的長度。
取何值時,污水凈化效果最好?并求出此時管道的長度。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)已知![]() 是定義在
是定義在![]() 上的奇函數,且
上的奇函數,且![]() ,當
,當![]()
![]() ,
,![]() 時,有
時,有![]() 成立.
成立.
(Ⅰ)判斷![]() 在
在![]() 上的單調性,并加以證明;
上的單調性,并加以證明;
(Ⅱ)若![]() 對所有的
對所有的![]() 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】傳承傳統文化再掀熱潮,央視科教頻道以詩詞知識競賽為主的《中國詩詞大會》火爆熒屏,將中學組和大學組的參賽選手按成績分為優秀、良好、一般三個等級,隨機從中抽取了100名選手進行調查,下面是根據調查結果繪制的選手等級人數的條形圖.
(1)若將一般等級和良好等級合稱為合格等級,根據已知條件完成下面的![]() 列聯表,并據此資料你是否有95%的把握認為選手成績“優秀”與文化程度有關?
列聯表,并據此資料你是否有95%的把握認為選手成績“優秀”與文化程度有關?


(2)若參賽選手共6萬人,用頻率估計概率,試估計其中優秀等級的選手人數;
(3)在優秀等級的選手中取6名,依次編號為1,2,3,4,5,6,在良好等級的選手中取6名,依次編號為1,2,3,4,5,6,在選出的6名優秀等級的選手中任取一名,記其編號為![]() ,在選出的6名良好等級的選手中任取一名,記其編號為
,在選出的6名良好等級的選手中任取一名,記其編號為![]() ,求使得方程組
,求使得方程組![]() 有唯一一組實數解
有唯一一組實數解![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數(Air Quality Index,簡稱![]() )是定量描述空氣質量狀況的指數,空氣質量按照
)是定量描述空氣質量狀況的指數,空氣質量按照![]() 大小分為六級,
大小分為六級,![]() 為優;
為優;![]() 為輕度污染;
為輕度污染;![]() 為中度污染;
為中度污染;![]() 為重度污染;
為重度污染;![]() 為嚴重污染.一環保人士記錄去年某地某月10天的
為嚴重污染.一環保人士記錄去年某地某月10天的![]() 的莖葉圖如右.
的莖葉圖如右.
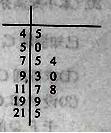
(1)利用該樣本估計該地本月空氣質量優良(![]() )的天數;(按這個月總共30天計算)
)的天數;(按這個月總共30天計算)
(2)將頻率視為概率,從本月中隨機抽取3天,記空氣質量優良的天數為![]() ,求
,求![]() 的概率分布列和數學期望.
的概率分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在五棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() .
.
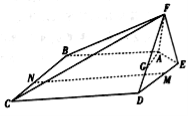
(1)已知點![]() 在線段
在線段![]() 上,確定
上,確定![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)點![]() 分別在線段
分別在線段![]() 上,若沿直線
上,若沿直線![]() 將四邊形
將四邊形![]() 向上翻折,
向上翻折,![]() 與
與![]() 恰好重合,求直線
恰好重合,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com