
【題目】如圖:某污水處理廠要在一個矩形污水處理池(![]() )的池底水平鋪設污水凈化管道(
)的池底水平鋪設污水凈化管道(![]() 是直角頂點)來處理污水,管道越長污水凈化效果越好,設計要求管道的的接口
是直角頂點)來處理污水,管道越長污水凈化效果越好,設計要求管道的的接口![]() 是
是![]() 的中點,
的中點,![]() 分別落在線段
分別落在線段![]() 上。已知
上。已知![]() 米,
米,![]() 米,記
米,記![]() .
.
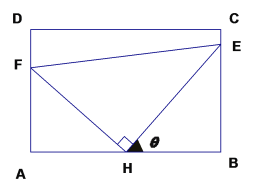
(1)試將污水凈化管道的長度![]() 表示為
表示為![]() 的函數,并寫出定義域;
的函數,并寫出定義域;
(2)若![]() ,求此時管道的長度
,求此時管道的長度![]() ;
;
(3)當![]() 取何值時,污水凈化效果最好?并求出此時管道的長度。
取何值時,污水凈化效果最好?并求出此時管道的長度。
 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:高中數學 來源: 題型:
【題目】根據國家環保部新修訂的《環境空氣質量標準》規定:居民區![]() 的年平均濃度不得超過
的年平均濃度不得超過![]() 微克/立方米,
微克/立方米,![]() 的24小時平均濃度不得超過
的24小時平均濃度不得超過![]() 微克/立方米.某城市環保部門隨機抽取了一居民區去年20天
微克/立方米.某城市環保部門隨機抽取了一居民區去年20天![]() 的24小時平均濃度的監測數據,數據統計如下:
的24小時平均濃度的監測數據,數據統計如下:
組別 |
(微克/立方米) | 頻數(天) | 頻率 |
第一組 |
| 3 | 0.15 |
第二組 |
| 12 | 0.6 |
第三組 |
| 3 | 0.15 |
第四組 |
| 2 | 0.1 |
(1)從樣本中![]() 的24小時平均濃度超過50微克/立方米的5天中,隨機抽取2天,求恰好有一天
的24小時平均濃度超過50微克/立方米的5天中,隨機抽取2天,求恰好有一天
![]() 的24小時平均濃度超過75微克/立方米的概率;
的24小時平均濃度超過75微克/立方米的概率;
(2)求樣本平均數,并根據樣本估計總體的思想,從![]() 的年平均濃度考慮,判斷該居民區的環境是
的年平均濃度考慮,判斷該居民區的環境是
否需要改進?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足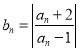 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表達式(不必寫出證明過程);
的表達式(不必寫出證明過程);
(2)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
(B)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表達式(不必寫出證明過程);
的表達式(不必寫出證明過程);
(2)設![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
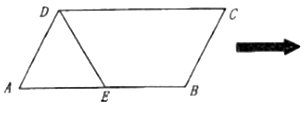
【題目】已知平行四邊形![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點,且△
的中點,且△![]() 是等邊三角形,沿
是等邊三角形,沿![]() 把△
把△![]() 折起至
折起至![]() 的位置,使得
的位置,使得![]() .
.
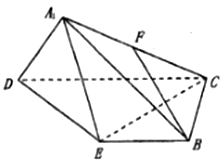
(1)![]() 是線段
是線段![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)求證:![]() ;
;
(3)求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(A)已知數列![]() 滿足
滿足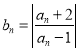 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表達式(不必寫出證明過程);
的表達式(不必寫出證明過程);
(2)由(1)寫出數列![]() 的前
的前![]() 項和
項和![]() ,并用數學歸納法證明.
,并用數學歸納法證明.
(B)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,
, ![]() .
.
(1)猜想![]() 的表達式,并用數學歸納法證明;
的表達式,并用數學歸納法證明;
(2)設![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A(4,-3),B(2,-1)和直線l:4x+3y-2=0.
(1)求在直角坐標平面內滿足|PA|=|PB|的點P的方程;
(2)求在直角坐標平面內一點P滿足|PA|=|PB|且點P到直線l的距離為2的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com