
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的圖象在
的圖象在![]() 處的切線方程;
處的切線方程;
(2)討論函數![]() 的單調性;
的單調性;
(3)當![]() 時,若方程
時,若方程![]() 有兩個不相等的實數根
有兩個不相等的實數根![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時,![]() 在
在![]() 上是減函數;當
上是減函數;當![]() 時,
時,![]() 在
在![]() 上是增函數;(3)證明見解析.
上是增函數;(3)證明見解析.
【解析】
(1)當![]() 時,
時,![]() ,求得其導函數
,求得其導函數 ![]() ,
,![]() ,可求得函數
,可求得函數![]() 的圖象在
的圖象在![]() 處的切線方程;
處的切線方程;
(2)由已知得![]() ,得出導函數
,得出導函數![]() ,并得出導函數取得正負的區間,可得出函數的單調性;
,并得出導函數取得正負的區間,可得出函數的單調性;
(3)當![]() 時,
時,![]() ,
,![]() ,由(2)得
,由(2)得![]() 的單調區間,以當方程
的單調區間,以當方程![]() 有兩個不相等的實數根
有兩個不相等的實數根![]() ,不妨設
,不妨設![]() ,且有
,且有![]() ,
,![]() ,構造函數
,構造函數![]() ,分析其導函數的正負得出函數的單調性,得出其最值,所證的不等式可得證.
,分析其導函數的正負得出函數的單調性,得出其最值,所證的不等式可得證.
(1)當![]() 時,
時,![]() ,
,
所以 ![]() ,
,![]() ,
,
所以函數![]() 的圖象在
的圖象在![]() 處的切線方程為
處的切線方程為![]() ,即
,即![]() ;
;
(2)由已知得![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,
,
所以當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數;
上是增函數;
(3)當![]() 時,
時,![]() ,
,![]() ,由(2)得
,由(2)得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增,
單調遞增,
所以![]() ,且
,且![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,![]() ,
,
所以當方程![]() 有兩個不相等的實數根
有兩個不相等的實數根![]() ,不妨設
,不妨設![]() ,且有
,且有![]() ,
,![]() ,
,
構造函數![]() ,則
,則![]() ,
,
當![]() 時,
時,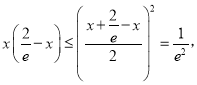 所以
所以![]() ,
,
![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]() ,
,![]() ,
,
由![]()
![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() .
.
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,以下結論正確的個數為( )
,以下結論正確的個數為( )
①當![]() 時,函數
時,函數![]() 的圖象的對稱中心為
的圖象的對稱中心為![]() ;
;
②當![]() 時,函數
時,函數![]() 在
在![]() 上為單調遞減函數;
上為單調遞減函數;
③若函數![]() 在
在![]() 上不單調,則
上不單調,則![]() ;
;
④當![]() 時,
時,![]() 在
在![]() 上的最大值為15.
上的最大值為15.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車生產企業上年度生產一品牌汽車的投入成本為10萬元/輛,出廠價為14萬元/輛,年銷售量為![]() 輛.本年度為適應市場需求,計劃提高產品檔次,適當增加投入成本,若每輛車投入成本增加的比例為
輛.本年度為適應市場需求,計劃提高產品檔次,適當增加投入成本,若每輛車投入成本增加的比例為![]() (0<
(0<![]() <1),則出廠價相應提高的比例為0.6
<1),則出廠價相應提高的比例為0.6![]() ,年銷售量也相應增加.已知年利潤=(每輛車的出廠價-每輛車的投入成本)×年銷售量.
,年銷售量也相應增加.已知年利潤=(每輛車的出廠價-每輛車的投入成本)×年銷售量.
(1)若年銷售量增加的比例為0.5![]() ,為使本年度的年利潤比上年度有所增加,則投入成本增加的比例
,為使本年度的年利潤比上年度有所增加,則投入成本增加的比例![]() 應在什么范圍內?
應在什么范圍內?
(2)若年銷售量關于![]() 的函數為
的函數為![]() 為常數),則當
為常數),則當![]() 為何值時,本年度的年利潤最大?
為何值時,本年度的年利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 為等邊三角形,且垂直于底面
為等邊三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)已知點![]() 在棱
在棱![]() 上且
上且![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別是△ABC的內角A,B,C的對邊,若△ABC的周長為2(![]() +1),且sin B+sin C=
+1),且sin B+sin C=![]() sin A,則a= ( )
sin A,則a= ( )
A. ![]() B. 2 C. 4 D.
B. 2 C. 4 D. ![]()
【答案】B
【解析】
根據正弦定理把![]() 轉化為邊的關系,進而根據△ABC的周長,聯立方程組,可求出a的值.
轉化為邊的關系,進而根據△ABC的周長,聯立方程組,可求出a的值.
根據正弦定理,![]() 可化為
可化為![]()
∵△ABC的周長為![]() ,
,
∴聯立方程組![]() ,
,
解得a=2.
故選:B
【點睛】
(1)在三角形中根據已知條件求未知的邊或角時,要靈活選擇正弦、余弦定理進行邊角之間的轉化,以達到求解的目的.
(2)求角的大小時,在得到角的某一個三角函數值后,還要根據角的范圍才能確定角的大小,這點容易被忽視,解題時要注意.
【題型】單選題
【結束】
7
【題目】已知數列{an}中,an=n2-kn(n∈N*),且{an}單調遞增,則k的取值范圍是( )
A. (-∞,2] B. (-∞,2) C. (-∞,3] D. (-∞,3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在學習強國活動中,某市圖書館的科技類圖書和時政類圖書是市民借閱的熱門圖書.為了豐富圖書資源,現對已借閱了科技類圖書的市民(以下簡稱為“問卷市民”)進行隨機問卷調查,若不借閱時政類圖書記1分,若借閱時政類圖書記2分,每位市民選擇是否借閱時政類圖書的概率均為![]() ,市民之間選擇意愿相互獨立.
,市民之間選擇意愿相互獨立.
(1)從問卷市民中隨機抽取4人,記總得分為隨機變量![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)(i)若從問卷市民中隨機抽取![]() 人,記總分恰為
人,記總分恰為![]() 分的概率為
分的概率為![]() ,求數列
,求數列![]() 的前10項和;
的前10項和;
(ⅱ)在對所有問卷市民進行隨機問卷調查過程中,記已調查過的累計得分恰為![]() 分的概率為
分的概率為![]() (比如:
(比如:![]() 表示累計得分為1分的概率,
表示累計得分為1分的概率,![]() 表示累計得分為2分的概率,
表示累計得分為2分的概率,![]() ),試探求
),試探求![]() 與
與![]() 之間的關系,并求數列
之間的關系,并求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據說,年過半百的笛卡爾擔任瑞典一小公國的公主克里斯蒂娜的數學老師,日久生情,彼此愛慕,其父國王知情后大怒,將笛卡爾流放回法國,并軟禁公主,笛卡爾回法國后染上黑死病,連連給公主寫信,死前最后一封信只有一個公式:![]()
![]() 國王不懂,將這封信交給了公主,公主用笛卡爾教她的坐標知識,畫出了這個圖形“心形線”.明白了笛卡爾的心意,登上了國王寶座后,派人去尋笛卡爾,其逝久矣(僅是一個傳說).心形線是由一個圓上的一個定點,當該圓繞著與其相切且半徑相同的另外一個圓周上滾動時,這個定點的軌跡,因其形狀像心形而得名.在極坐標系
國王不懂,將這封信交給了公主,公主用笛卡爾教她的坐標知識,畫出了這個圖形“心形線”.明白了笛卡爾的心意,登上了國王寶座后,派人去尋笛卡爾,其逝久矣(僅是一個傳說).心形線是由一個圓上的一個定點,當該圓繞著與其相切且半徑相同的另外一個圓周上滾動時,這個定點的軌跡,因其形狀像心形而得名.在極坐標系![]() 中,方程
中,方程![]()
![]() 表示的曲線
表示的曲線![]() 就是一條心形線,如圖,以極軸
就是一條心形線,如圖,以極軸![]() 所在直線為
所在直線為![]() 軸,極點
軸,極點![]() 為坐標原點的直角坐標系
為坐標原點的直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為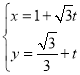 (
(![]() 為參數).
為參數).
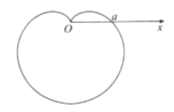
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)若曲線![]() 與
與![]() 相交于
相交于![]() 、
、![]() 、
、![]() 三點,求線段
三點,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
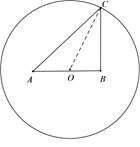
【題目】某公園準備在一圓形水池里設置兩個觀景噴泉,觀景噴泉的示意圖如圖所示,![]() 兩點為噴泉,圓心
兩點為噴泉,圓心![]() 為
為![]() 的中點,其中
的中點,其中![]() 米,半徑
米,半徑![]() 米,市民可位于水池邊緣任意一點
米,市民可位于水池邊緣任意一點![]() 處觀賞.
處觀賞.
(1)若當![]() 時,
時,![]() ,求此時
,求此時![]() 的值;
的值;
(2)設![]() ,且
,且![]() .
.
(i)試將![]() 表示為
表示為![]() 的函數,并求出
的函數,并求出![]() 的取值范圍;
的取值范圍;
(ii)若同時要求市民在水池邊緣任意一點![]() 處觀賞噴泉時,觀賞角度
處觀賞噴泉時,觀賞角度![]() 的最大值不小于
的最大值不小于![]() ,試求
,試求![]() 兩處噴泉間距離的最小值.
兩處噴泉間距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為: ![]() (
(![]() 為參數,
為參數, ![]() ),將曲線
),將曲線![]() 經過伸縮變換:
經過伸縮變換:  得到曲線
得到曲線![]() .
.
(1)以原點為極點, ![]() 軸的正半軸為極軸建立坐標系,求
軸的正半軸為極軸建立坐標系,求![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() (
(![]() 為參數)與
為參數)與![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com