
【題目】已知平面內點![]() 到點
到點![]() 的距離和到直線
的距離和到直線![]() 的距離之比為
的距離之比為![]() ,若動點P的軌跡為曲線C.
,若動點P的軌跡為曲線C.
(I)求曲線C的方程;
(II)過F的直線![]() 與C交于A,B兩點,點M的坐標為
與C交于A,B兩點,點M的坐標為![]() 設O為坐標原點.證明:
設O為坐標原點.證明:![]() .
.
【答案】(I)![]() (II)見解析
(II)見解析
【解析】
(I)根據題目點![]() 到點
到點![]() 的距離和到直線
的距離和到直線![]() 的距離之比為
的距離之比為![]() ,列出相應的等式方程,化簡可得軌跡C的方程;
,列出相應的等式方程,化簡可得軌跡C的方程;
(II)對直線![]() 分
分![]() 軸、l與x軸重合以及l存在斜率且斜率不為零三種情況進行分析,當l存在斜率且斜率不為零時,利用點斜式設直線方程,與曲線C的方程進行聯立,結合韋達定理,可推得
軸、l與x軸重合以及l存在斜率且斜率不為零三種情況進行分析,當l存在斜率且斜率不為零時,利用點斜式設直線方程,與曲線C的方程進行聯立,結合韋達定理,可推得![]() ,從而推出
,從而推出![]() 。
。
解:(I)∵![]() 到點
到點![]() 的距離和到直線
的距離和到直線![]() 的距離之比為
的距離之比為![]() .
.
∴ ,
,![]() .
.
化簡得:![]() .
.
故所求曲線C的方程為:![]() .
.
(II)分三種情況討論:
1、當![]() 軸時,由橢圓對稱性易知:
軸時,由橢圓對稱性易知:![]() .
.
2、當l與x軸重合時,由直線與橢圓位置關系知:![]()
3、設l為:![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,
由 化簡得:
化簡得:![]() ,
,
∴![]() ,
,![]()
設MA,MB,所在直線斜率分別為:![]() ,
,![]() ,則
,則
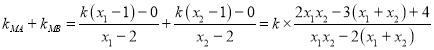

![]()
![]()
此時,![]() .
.
綜上所述:![]() .
.


科目:高中數學 來源: 題型:
【題目】假設有5個條件類似的女孩(把她們分別記為A,B,C,D, E)應聘秘書工作,但只有2個秘書職位,因此5個人中只有2人能被錄用.如果5個人被錄用的機會相等,分別計算下列事件的概率;
(1)女孩A得到一個職位;
(2)女孩A和B各得到一個職位;
(3)女孩A或B得到一個職位.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知離心率為![]() 的橢圓C:
的橢圓C:![]() (a>b>0)的左焦點為
(a>b>0)的左焦點為![]() ,過
,過![]() 作長軸的垂線交橢圓于
作長軸的垂線交橢圓于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(I)求橢圓C的標準方程;
(II)設O為原點,若點A在直線![]() 上,點B在橢圓C上,且
上,點B在橢圓C上,且![]() ,求線段AB長度的最小值.
,求線段AB長度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知點A是拋物線![]() 的對稱軸與準線的交點,點B為拋物線的焦點,P在拋物線上且滿足
的對稱軸與準線的交點,點B為拋物線的焦點,P在拋物線上且滿足![]() ,當
,當![]() 取最大值時,點P恰好在以A、B為焦點的雙曲線上,則雙曲線的離心率為
取最大值時,點P恰好在以A、B為焦點的雙曲線上,則雙曲線的離心率為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司試銷一種成本單價為500元/件的新產品,規定試銷時銷售單價不低于成本單價,又不高于800元/件.經試銷調查,發現銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元/件)可近似看作一次函數
(元/件)可近似看作一次函數![]() 的關系(如圖所示).
的關系(如圖所示).

(1)由圖象,求函數![]() 的表達式;
的表達式;
(2)設公司獲得的毛利潤(毛利潤=銷售總價﹣成本總價)為![]() 元.試用銷售單價
元.試用銷售單價![]() 表示毛利潤
表示毛利潤![]() ,并求銷售單價定為多少時,該公司獲得最大毛利潤?最大毛利潤是多少?此時的銷售量是多少?
,并求銷售單價定為多少時,該公司獲得最大毛利潤?最大毛利潤是多少?此時的銷售量是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果l是空間中的一條直線,![]() 是空間中的一個平面,判斷下列命題的真假.
是空間中的一個平面,判斷下列命題的真假.
(1)l與![]() 要么相交,要么不相交;
要么相交,要么不相交;
(2)要么l在![]() 內,要么l在
內,要么l在![]() 外;
外;
(3)要么l與![]() 平行,要么l在
平行,要么l在![]() 內.
內.
查看答案和解析>>
科目:高中數學 來源: 題型:
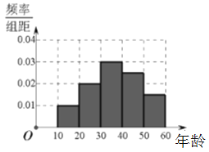
【題目】中國已經成為全球最大的電商市場,但是實體店仍然是消費者接觸商品和品牌的重要渠道.某機構隨機抽取了年齡介于10歲到60歲的消費者200人,對他們的主要購物方式進行問卷調查.現對調查對象的年齡分布及主要購物方式進行統計,得到如下圖表:
主要購物方式 年齡階段 | 網絡平臺購物 | 實體店購物 | 總計 |
40歲以下 | 75 | ||
40歲或40歲以上 | 55 | ||
總計 |
(1)根據已知條件完成上述列聯表,并據此資料,能否在犯錯誤的概率不超過![]() 的前提下,認為消費者主要的購物方式與年齡有關?
的前提下,認為消費者主要的購物方式與年齡有關?
(2)用分層抽樣的方法從通過網絡平臺購物的消費者中隨機抽取8人,然后再從這8名消費者中抽取5名進行答謝.設抽到的消費者中40歲以下的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式: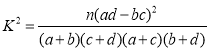 ,其中
,其中![]() .
.
臨界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com