
【題目】已知函數![]() 是定義在R上的奇函數,
是定義在R上的奇函數,
(1)求實數![]() 的值;
的值;
(2)如果對任意![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
 培優(yōu)三好生系列答案
培優(yōu)三好生系列答案 優(yōu)化作業(yè)上海科技文獻出版社系列答案
優(yōu)化作業(yè)上海科技文獻出版社系列答案科目:高中數學 來源: 題型:
【題目】已知平面內點![]() 到點
到點![]() 的距離和到直線
的距離和到直線![]() 的距離之比為
的距離之比為![]() ,若動點P的軌跡為曲線C.
,若動點P的軌跡為曲線C.
(I)求曲線C的方程;
(II)過F的直線![]() 與C交于A,B兩點,點M的坐標為
與C交于A,B兩點,點M的坐標為![]() 設O為坐標原點.證明:
設O為坐標原點.證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某市舉行的一次市質檢考試中,為了調查考試試題的有效性以及試卷的區(qū)分度,該市教研室隨機抽取了參加本次質檢考試的500名學生的數學考試成績,并將其統(tǒng)計如下表所示.

根據上表數據統(tǒng)計,可知考試成績落在![]() 之間的頻率為
之間的頻率為![]() .
.
(Ⅰ)求m、n的值;
(Ⅱ)已知本歡質檢中的數學測試成績![]() ,其中
,其中![]() 近似為樣本的平均數,
近似為樣本的平均數,![]() 近似為樣本方差
近似為樣本方差![]() ,若該市有4萬考生,試估計數學成績介于
,若該市有4萬考生,試估計數學成績介于![]() 分的人數;
分的人數;![]() 以各組的區(qū)間的中點值代表該組的取值
以各組的區(qū)間的中點值代表該組的取值![]() Ⅲ
Ⅲ![]() 現按分層抽樣的方法從成績在
現按分層抽樣的方法從成績在![]() 以及
以及![]() 之間的學生中隨機抽取12人,再從這12人中隨機抽取4人進行試卷分析,記被抽取的4人中成績在
之間的學生中隨機抽取12人,再從這12人中隨機抽取4人進行試卷分析,記被抽取的4人中成績在![]() 之間的人數為X,求X的分布列以及期望
之間的人數為X,求X的分布列以及期望![]() .
.
參考數據:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過點![]() 的直線
的直線![]() 的參數方程是
的參數方程是 (
(![]() 為參數),以平面直角坐標系的原點為極點,
為參數),以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,試問是否存在實數
兩點,試問是否存在實數![]() ,使得
,使得![]() ?若存在,求出實數
?若存在,求出實數![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)如圖,在邊長為![]() 的菱形
的菱形![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 的中點,
的中點,![]() .沿
.沿![]() 將△
將△![]() 翻折到△
翻折到△![]() ,連接
,連接![]() ,得到如圖的五棱錐
,得到如圖的五棱錐![]() ,且
,且![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代有著輝煌的數學研究成果,其中的《周髀算經》、《九章算術》、《海島算經》、《孫子算經》、《緝古算經》,有豐富多彩的內容,是了解我國古代數學的重要文獻,這5部專著中有3部產生于漢、魏、晉、南北朝時期,某中學擬從這5部專著中選擇2部作為“數學文化”校本課程學習內容,則所選2部專著中至少有一部是漢、魏、晉、南北朝時期專著的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個電路中有A,B,C三個電器元件,每個元件可能正常,也可能失效,把這個電路是否為通路看成是一個隨機現象,觀察這個電路中各元件是否正常.

(1)寫出試驗的樣本空間;
(2)用集合表示下列事件:M=“恰好兩個元件正常”;N=“電路是通路”;T=“電路是斷路”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD是一個菱形,三角形PAD是一個等腰三角形,∠BAD=∠PAD=![]() ,點E在線段PC上,且PE=3EC.
,點E在線段PC上,且PE=3EC.
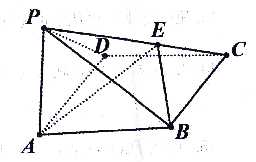
(1)求證:AD⊥PB;
(2)若平面PAD⊥平面ABCD,求二面角E﹣AB﹣P的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正六棱錐![]() 的底面邊長為
的底面邊長為![]() ,高為
,高為![]() .現從該棱錐的
.現從該棱錐的![]() 個頂點中隨機選取
個頂點中隨機選取![]() 個點構成三角形,設隨機變量
個點構成三角形,設隨機變量![]() 表示所得三角形的面積.
表示所得三角形的面積.
(1)求概率![]() 的值;
的值;
(2)求![]() 的分布列,并求其數學期望
的分布列,并求其數學期望![]() .
.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com