【題目】如圖，A是△BCD所在平面外一點，M、N為△ABC和△ACD重心，BD=6； 
（1）求MN的長；
（2）若A、C的位置發生變化，MN的位置和長度會改變嗎？
【答案】
（1）解：延長AM、AN，分別交BC、CD于點E、F，連結EF．
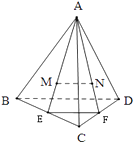
∵M、N分別是△ABC和△ACD的重心，
∴AE、AF分別為△ABC和△ACD的中線，且 
= 
，
可得MN∥EF且MN= EF，
∵EF為△BCD的中位線，可得EF= 
BD，
∴MN= 
BD=2
（2）解：由（1）可得位置改變，長度不改變．
【解析】（1）利用三角形的重心的性質，可得M、N分別是△ABC與△ACD的中線的一個三等分點，得 = ，由此利用平行線的性質與三角形中位線定理，算出MN與BD的關系，即可得到MN的長．（2）由（1）可得位置改變，長度不改變．
【考點精析】本題主要考查了棱錐的結構特征的相關知識點，需要掌握側面、對角面都是三角形；平行于底面的截面與底面相似，其相似比等于頂點到截面距離與高的比的平方才能正確解答此題．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】給出下列4個命題
①“若
，則
”的否命題是“若
，則
”；
②若命題
，則
為真命題；
③“平面向量
夾角為銳角，則
”的逆命題為真命題；
④“函數
有零點”是“函數
在
上為減函數”的充要條件.
其中正確的命題個數是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）是二次函數，且滿足f（0）=1，f（x+1）﹣f（x）=2x+5；函數g（x）=ax（a＞0且a≠1）
（1）求f（x）的解析式；
（2）若g（2）= 
，且g[f（x）]≥k對x∈[﹣1，1]恒成立，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我們把b除a的余數r記為r=abmodb，例如4=9bmod5，如圖所示，若輸入a=209，b=77，則循環體“r←abmodb”被執行了次．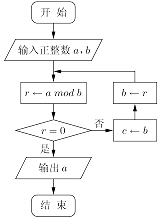 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和Sn滿足：Sn= 
（an﹣1）（a為常數，且a≠0，a≠1）；
（1）求{an}的通項公式；
（2）設bn= 
+1，若數列{bn}為等比數列，求a的值；
（3）若數列{bn}是（2）中的等比數列，數列cn=（n﹣1）bn ， 求數列{cn}的前n項和Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在等差數列
中， 
，其前
項和為
，等比數列
的各項均為正數， 
，且
， 
.
（1）求數列
和
的通項公式；
（2）令
，設數列
的前
項和為
，求
（
）的最大值與最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=a﹣ 
，
（1）若x∈[ 
，+∞），①判斷函數g（x）=f（x）﹣2x的單調性并加以證明；②如果f（x）≤2x恒成立，求a的取值范圍；
（2）若總存在m，n使得當x∈[m，n]時，恰有f（x）∈[2m，2n]，求a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
