
【題目】給出下列4個命題
①“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”;
”;
②若命題![]() ,則
,則![]() 為真命題;
為真命題;
③“平面向量![]() 夾角為銳角,則
夾角為銳角,則![]() ”的逆命題為真命題;
”的逆命題為真命題;
④“函數![]() 有零點”是“函數
有零點”是“函數![]() 在
在![]() 上為減函數”的充要條件.
上為減函數”的充要條件.
其中正確的命題個數是( )
A. 1 B. 2 C. 3 D. 4
 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:
【題目】某景點擬建一個扇環形狀的花壇(如圖所示),按設計要求扇環的周長為36米,其中大圓弧所在圓的半徑為14米,設小圓弧所在圓的半徑為![]() 米,圓心角為
米,圓心角為![]() (弧度).
(弧度).
⑴ 求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
⑵ 已知對花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為16元/米,設花壇的面積與裝飾總費用之比為![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并求出
的函數關系式,并求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,互相垂直的兩條公路AP、AQ旁有一矩形花園ABCD,現欲將其擴建成一個更大的三角形花園AMN,要求點M在射線AP上,點N在射線AQ上,且直線MN過點C,其中AB=36米,AD=20米.記三角形花園AMN的面積為S. (Ⅰ)問:DN取何值時,S取得最小值,并求出最小值;
(Ⅱ)若S不超過1764平方米,求DN長的取值范圍.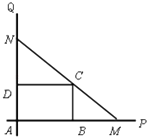
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是定義在
是定義在![]() 上的奇函數.
上的奇函數.
(1)當![]() 時,
時, ![]() ,若當
,若當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)若![]() 的圖像關于
的圖像關于![]() 對稱,且
對稱,且![]() 時,
時, ![]() ,求當
,求當![]() 時,
時, ![]() 的解析式;
的解析式;
(3)當![]() 時,
時, ![]() .若對任意的
.若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,A是△BCD所在平面外一點,M、N為△ABC和△ACD重心,BD=6; 
(1)求MN的長;
(2)若A、C的位置發生變化,MN的位置和長度會改變嗎?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com