
【題目】設(shè)函數(shù)f(x)=a﹣ ![]() ,
,
(1)若x∈[ ![]() ,+∞),①判斷函數(shù)g(x)=f(x)﹣2x的單調(diào)性并加以證明;②如果f(x)≤2x恒成立,求a的取值范圍;
,+∞),①判斷函數(shù)g(x)=f(x)﹣2x的單調(diào)性并加以證明;②如果f(x)≤2x恒成立,求a的取值范圍;
(2)若總存在m,n使得當(dāng)x∈[m,n]時(shí),恰有f(x)∈[2m,2n],求a的取值范圍.
【答案】
(1)解:①x∈[ ![]() ,+∞)時(shí),g(x)=f(x)﹣2x=a﹣
,+∞)時(shí),g(x)=f(x)﹣2x=a﹣ ![]() .
.
任取 ![]() ,
,
![]() =
= ![]() .
.
∵ ![]() ,∴x2﹣x10,x1x2>0.
,∴x2﹣x10,x1x2>0.
∴g(x1)﹣g(x2)<0,g(x1)<g(x2).
∴g(x)在[ ![]() ,+∞)上單調(diào)遞減.
,+∞)上單調(diào)遞減.
②f(x)≤2xg(x)≤0,∵g(x)在[ ![]() ,+∞)上單調(diào)遞減,
,+∞)上單調(diào)遞減,
∴ ![]() ,∴
,∴ ![]()
(2)解:∵f(x)=a﹣ ![]() 的定義域?yàn)椋ī仭蓿?)∪(0,+∞),∴mn>0
的定義域?yàn)椋ī仭蓿?)∪(0,+∞),∴mn>0
若n>m>0,則 ![]() ,且在[m,n]上遞增,∴
,且在[m,n]上遞增,∴ ![]() ,∴
,∴ 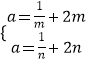 .
.
∴m,n是 ![]() 的兩個(gè)根,即2x2﹣ax+1=0的兩個(gè)根,
的兩個(gè)根,即2x2﹣ax+1=0的兩個(gè)根,
∴ 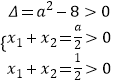 ,解得
,解得 ![]() .
.
若m<n<0,則f(x)=a+ ![]() ,且在[m,n]上遞減,
,且在[m,n]上遞減,
∴ ![]() ,∴
,∴ 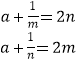 ,相減得:mn=
,相減得:mn= ![]() ,代回得:a=0.
,代回得:a=0.
綜上所得:a的取值范圍是( ![]() )∪{0}
)∪{0}
【解析】(1)①把f(x)的解析式代入后,直接利用函數(shù)的單調(diào)性的定義證明;②由①中的單調(diào)性求出g(x)的最大值,由最大值小于等于0求解a的范圍;(2)求出函數(shù)的定義域,然后分m,n同正和同負(fù)兩種情況分析,借助于函數(shù)的單調(diào)性的方程組,然后再轉(zhuǎn)化為方程的根進(jìn)行分析.
【考點(diǎn)精析】解答此題的關(guān)鍵在于理解函數(shù)單調(diào)性的判斷方法的相關(guān)知識(shí),掌握單調(diào)性的判定法:①設(shè)x1,x2是所研究區(qū)間內(nèi)任兩個(gè)自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較.


 世紀(jì)百通主體課堂小學(xué)課時(shí)同步達(dá)標(biāo)系列答案
世紀(jì)百通主體課堂小學(xué)課時(shí)同步達(dá)標(biāo)系列答案 世紀(jì)百通優(yōu)練測(cè)系列答案
世紀(jì)百通優(yōu)練測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知圓C的方程(x﹣1)2+y2=1,P是橢圓 ![]() =1上一點(diǎn),過(guò)P作圓的兩條切線(xiàn),切點(diǎn)為A,B,則
=1上一點(diǎn),過(guò)P作圓的兩條切線(xiàn),切點(diǎn)為A,B,則 ![]() 的取值范圍為( )
的取值范圍為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,A是△BCD所在平面外一點(diǎn),M、N為△ABC和△ACD重心,BD=6; 
(1)求MN的長(zhǎng);
(2)若A、C的位置發(fā)生變化,MN的位置和長(zhǎng)度會(huì)改變嗎?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若函數(shù)![]() 在其定義域內(nèi)為增函數(shù),求實(shí)數(shù)
在其定義域內(nèi)為增函數(shù),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)設(shè)函數(shù)![]() ,若在
,若在![]() 上至少存在一點(diǎn)
上至少存在一點(diǎn)![]() ,使得
,使得![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的極大值;
的極大值;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]()
![]() 其中
其中![]() 上存在極值,求實(shí)數(shù)
上存在極值,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)如果當(dāng)![]() 時(shí),不等式
時(shí),不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】從裝有大小相同的2個(gè)紅球和6個(gè)白球的袋子中,每摸出2個(gè)球?yàn)橐淮卧囼?yàn),直到摸出的球中有紅球(不放回),則試驗(yàn)結(jié)束.
(1)求第一次試驗(yàn)恰摸到一個(gè)紅球和一個(gè)白球概率;
(2)記試驗(yàn)次數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望
的分布列及數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]()
(1)若![]() 在點(diǎn)
在點(diǎn)![]() 處的切線(xiàn)斜率為
處的切線(xiàn)斜率為![]() ,求
,求![]() 的值;
的值;
(2)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)若![]() ,求證:在
,求證:在![]() 時(shí),
時(shí), ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某餐廳裝修,需要大塊膠合板![]() 張,小塊膠合板
張,小塊膠合板![]() 張,已知市場(chǎng)出售
張,已知市場(chǎng)出售![]() 兩種不同規(guī)格的膠合板。經(jīng)過(guò)測(cè)算,
兩種不同規(guī)格的膠合板。經(jīng)過(guò)測(cè)算, ![]() 種規(guī)格的膠合板可同時(shí)截得大塊膠合板
種規(guī)格的膠合板可同時(shí)截得大塊膠合板![]() 張,小塊膠合板
張,小塊膠合板![]() 張,
張, ![]() 種規(guī)格的膠合板可同時(shí)截得大塊膠合板
種規(guī)格的膠合板可同時(shí)截得大塊膠合板![]() 張,小塊膠合板
張,小塊膠合板![]() 張.已知
張.已知![]() 種規(guī)格膠合板每張
種規(guī)格膠合板每張![]() 元,
元, ![]() 種規(guī)格膠合板每張
種規(guī)格膠合板每張![]() 元.分別用
元.分別用![]() 表示購(gòu)買(mǎi)
表示購(gòu)買(mǎi)![]() 兩種不同規(guī)格的膠合板的張數(shù).
兩種不同規(guī)格的膠合板的張數(shù).
(1)用![]() 列出滿(mǎn)足條件的數(shù)學(xué)關(guān)系式,并畫(huà)出相應(yīng)的平面區(qū)域;
列出滿(mǎn)足條件的數(shù)學(xué)關(guān)系式,并畫(huà)出相應(yīng)的平面區(qū)域;
(2)根據(jù)施工需求, ![]() 兩種不同規(guī)格的膠合板各買(mǎi)多少?gòu)埢ㄙM(fèi)資金最少?并求出最少資金數(shù).
兩種不同規(guī)格的膠合板各買(mǎi)多少?gòu)埢ㄙM(fèi)資金最少?并求出最少資金數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列命題中,正確的序號(hào)是 . ①y=﹣2cos( ![]() π﹣2x)是奇函數(shù);
π﹣2x)是奇函數(shù);
②若α,β是第一象限角,且α>β,則sinα>sinβ;
③x=﹣ ![]() 是函數(shù)y=3sin(2x﹣
是函數(shù)y=3sin(2x﹣ ![]() )的一條對(duì)稱(chēng)軸;
)的一條對(duì)稱(chēng)軸;
④函數(shù)y=sin( ![]() ﹣2x)的單調(diào)減區(qū)間是[kπ﹣
﹣2x)的單調(diào)減區(qū)間是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com