
【題目】三棱錐P﹣ABC中.AB⊥BC,△PAC為等邊三角形,二面角P﹣AC﹣B的余弦值為![]() ,當三棱錐的體積最大時,其外接球的表面積為8π.則三棱錐體積的最大值為( )
,當三棱錐的體積最大時,其外接球的表面積為8π.則三棱錐體積的最大值為( )
A.1B.2C.![]() D.
D.![]()
【答案】D
【解析】
由已知作出圖象,找出二面角![]() 的平面角,設出AB,BC,AC的長,即可求出三棱錐
的平面角,設出AB,BC,AC的長,即可求出三棱錐![]() 的高,然后利用基本不等式即可確定三棱錐體積的最大值(用含有AC長度的字母表示),再設出球心O,由球的表面積求得半徑,根據球的幾何性質,利用球心距,半徑,底面半徑之間的關系求得AC的長度,則三棱錐體積的最大值可求.
的高,然后利用基本不等式即可確定三棱錐體積的最大值(用含有AC長度的字母表示),再設出球心O,由球的表面積求得半徑,根據球的幾何性質,利用球心距,半徑,底面半徑之間的關系求得AC的長度,則三棱錐體積的最大值可求.
如圖所示,過點P作PE⊥面ABC,垂足為E,過點E作ED⊥AC交AC于點D,連接PD,
則∠PDE為二面角P﹣AC﹣B的平面角的補角,即有cos∠PDE![]() ,
,
易知AC⊥面PDE,則AC⊥PD,而△PAC為等邊三角形,
∴D為AC中點,
設AB=a,BC=b,AC![]() c,
c,
則PE=PDsin∠PDE![]() c
c![]() ,
,
故三棱錐P﹣ABC的體積為:V![]() ab
ab![]() ,
,
當且僅當a=b![]() 時,體積最大,此時B、D、E共線.
時,體積最大,此時B、D、E共線.
設三棱錐P﹣ABC的外接球的球心為O,半徑為R,
由已知,4πR2=8π,得R![]() .
.
過點O作OF⊥PE于F,則四邊形ODEF為矩形,
則OD=EF![]() ,ED=OF=PDcos∠PDE
,ED=OF=PDcos∠PDE![]() ,PE
,PE![]() ,
,
在Rt△PFO中,(![]() )2
)2![]() ,解得c=2.
,解得c=2.
∴三棱錐P﹣ABC的體積的最大值為:![]() .
.
故選:D.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某市《城市總體規劃(![]() 年)》提出到2035年實現“15分鐘社區生活圈”全覆蓋的目標,從教育與文化、醫療與養老、交通與購物、休閑與健身4個方面構建“15分鐘社區生活圈“指標體系,并依據“15分鐘社區生活圈”指數高低將小區劃分為:優質小區(指數為
年)》提出到2035年實現“15分鐘社區生活圈”全覆蓋的目標,從教育與文化、醫療與養老、交通與購物、休閑與健身4個方面構建“15分鐘社區生活圈“指標體系,并依據“15分鐘社區生活圈”指數高低將小區劃分為:優質小區(指數為![]() 、良好小區(指數為0.4-0.63、中等小區(指數為0.2~0.4)以及待改進小區(指數為0-0.2)4個等級.下面是三個小區4個方面指標值的調查數據:
、良好小區(指數為0.4-0.63、中等小區(指數為0.2~0.4)以及待改進小區(指數為0-0.2)4個等級.下面是三個小區4個方面指標值的調查數據:
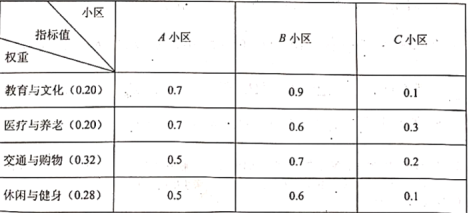
注:每個小區”15分鐘社區生活圈”指數![]() 其中
其中![]() 、
、![]() 、
、![]() 、
、![]() 為該小區四個方面的權重,
為該小區四個方面的權重,![]() 為該小區四個方面的指標值(小區每一個方面的指標值為
為該小區四個方面的指標值(小區每一個方面的指標值為![]() 之間的一個數值)
之間的一個數值)
現有100個小區的“15分鐘社區生活圈“指數數據,整理得到如下頻數分布表:

(1)分別判斷A、B、C三個小區是否是優質小區,并說明理由;
(2)對這100個小區按照優質小區、良好小區、中等小區和待改進小區進行分層抽樣,抽取10個小區進行調查,若在抽取的10個小區中再隨機地選取2個小區做深入調查,記這2個小區中為優質小區的個數為ζ,求ζ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】萬眾矚目的第14屆全國冬季運動運會(簡稱“十四冬”)于2020年2月16日在呼倫貝爾市盛大開幕,期間正值我市學校放寒假,寒假結束后,某校工會對全校100名教職工在“十四冬”期間每天收看比賽轉播的時間作了一次調查,得到如圖頻數分布直方圖:
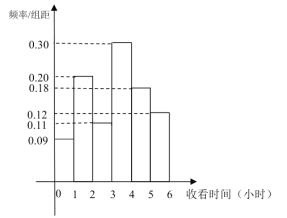
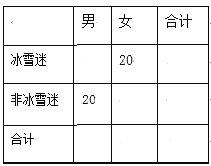
(1)若將每天收看比賽轉播時間不低于3小時的教職工定義為“冰雪迷”,否則定義為“非冰雪迷”,請根據頻率分布直方圖補全![]() 列聯表;并判斷能否有
列聯表;并判斷能否有![]() 的把握認為該校教職工是否為“冰雪迷”與“性別”有關;
的把握認為該校教職工是否為“冰雪迷”與“性別”有關;
(2)在全校“冰雪迷”中按性別分層抽樣抽取6名,再從這6名“冰雪迷”中選取2名作冰雪運動知識講座.記其中女職工的人數為![]() ,求的
,求的![]() 分布列與數學期望.
分布列與數學期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
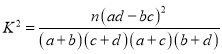 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,
為坐標原點,![]() 為坐標平面內動點,且
為坐標平面內動點,且![]() 成等差數列.
成等差數列.
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,過點
,過點![]() 作直線交
作直線交![]() 于
于![]() 兩點(不與原點重合),是否存在
兩點(不與原點重合),是否存在![]() 軸上一定點
軸上一定點![]() ,使得_________.若存在,求出定點
,使得_________.若存在,求出定點![]() ,若不存在,說明理由.從“①作
,若不存在,說明理由.從“①作![]() 點關于
點關于![]() 軸的對稱點
軸的對稱點![]() ,則
,則![]() 三點共線;②
三點共線;②![]() ”這兩個條件中選一個,補充在上面的問題中并作答(注:如果選擇兩個條件分別作答,按第一個解答計分)
”這兩個條件中選一個,補充在上面的問題中并作答(注:如果選擇兩個條件分別作答,按第一個解答計分)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明和父母都喜愛《中國好聲音》這欄節目,![]() 年
年![]() 月
月![]() 日晚在鳥巢進行中國好聲音終極決賽,四強選手分別為李榮浩戰隊的邢晗銘,那英戰隊的斯丹曼簇,王力宏戰隊的李芷婷,庾澄慶戰隊的陳其楠,決賽后四位選手相應的名次為
日晚在鳥巢進行中國好聲音終極決賽,四強選手分別為李榮浩戰隊的邢晗銘,那英戰隊的斯丹曼簇,王力宏戰隊的李芷婷,庾澄慶戰隊的陳其楠,決賽后四位選手相應的名次為![]() 、
、![]() 、
、![]() 、
、![]() ,某網站為提升娛樂性,邀請網友在比賽結束前對選手名次進行預測.現用
,某網站為提升娛樂性,邀請網友在比賽結束前對選手名次進行預測.現用![]() 、
、![]() 、
、![]() 、
、![]() 表示某網友對實際名次為
表示某網友對實際名次為![]() 、
、![]() 、
、![]() 、
、![]() 的四位選手名次做出的一種等可能的預測排列,
的四位選手名次做出的一種等可能的預測排列,![]() 是該網友預測的名次與真實名次的偏離程度的一種描述.
是該網友預測的名次與真實名次的偏離程度的一種描述.
(1)求![]() 的分布列及數學期望;
的分布列及數學期望;
(2)按(1)中的結果,若小明家三人的排序號與真實名次的偏離程度都是![]() ,計算出現這種情況的概率(假定小明家每個人排序相互獨立).
,計算出現這種情況的概率(假定小明家每個人排序相互獨立).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,國家為了鼓勵高校畢業生自主創業,出臺了許多優惠政策,以創業帶動就業.某高校畢業生小張自主創業從事蘋果的種植,并開設網店進行銷售.為了做好蘋果的品控,小張從自己果園的蘋果樹上,隨機摘取150個蘋果測重(單位:克),其重量分布在區間![]() 內,根據統計的數據得到如圖1所示的頻率分布直方圖.
內,根據統計的數據得到如圖1所示的頻率分布直方圖.
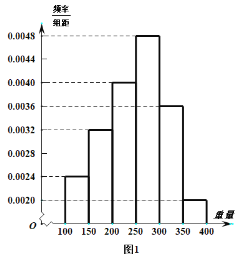
(1)以上述樣本數據中頻率作為概率,現一顧客從該果園購買了30個蘋果,求這30個蘋果中重量在![]() 內的個數
內的個數![]() 的數學期望;
的數學期望;
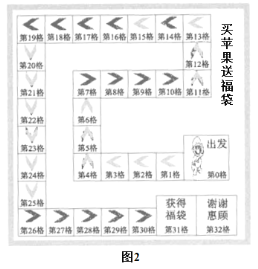
(2)小張的網店為了進行蘋果的促銷,推出了“買蘋果,送福袋”的活動,買家在線參加按圖行進贏取福袋的游戲.該游戲的規則如下:買家點擊拋擲一枚特殊的骰子,每次拋擲的結果為1或2,且這兩種結果的概率相同;從出發格(第0格)開始,每擲一次,按照拋擲的結果,按如圖2所示的路徑向前行進一次,若擲出1點,即從當前位置向前行進一格(從第![]() 格到第
格到第![]() 格,
格,![]() ),若擲出2點,即從當前位置向前行進兩格(從第
),若擲出2點,即從當前位置向前行進兩格(從第![]() 格到第
格到第![]() 格,
格,![]() ),行進至第3l格(獲得福袋)或第32格(謝謝惠顧),游戲結束.設買家行進至第
),行進至第3l格(獲得福袋)或第32格(謝謝惠顧),游戲結束.設買家行進至第![]() 格的概率為
格的概率為![]() ,
,![]() .
.
(ⅰ)求![]() 、
、![]() ,并寫出用
,并寫出用![]() 、
、![]() 表示
表示![]() 的遞推式;
的遞推式;
(ⅱ)求![]() ,并說明該大學生網店推出的此款游戲活動,是更有利于賣家,還是更有利于買家.
,并說明該大學生網店推出的此款游戲活動,是更有利于賣家,還是更有利于買家.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com