
【題目】已知函數![]() (
(![]() ,
, ![]() =2.718………),
=2.718………),
(I) 當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(II)當![]() 時,不等式
時,不等式![]() 對任意
對任意![]() 恒成立,
恒成立,
求實數![]() 的最大值.
的最大值.
【答案】(1)函數![]() 的單調遞增區間為
的單調遞增區間為![]() 和
和![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
(2)符合題意的實數![]() 的最大值為
的最大值為![]() .
.
【解析】試題分析:(1)求函數單調區間,即求導研究導函數的正負,導函數大于零求增區間,導函數小于零求減區間;(2)這是不等式恒成立求參的問題,轉化為![]() ,
, ![]() 對任意
對任意![]() 恒成立,再求導研究函數的單調性,求最值即可.
恒成立,再求導研究函數的單調性,求最值即可.
(1)![]()
由![]() 可知,
可知, ![]()
令![]() 得
得 ![]() 或
或![]()
令![]() 得
得 ![]()
即 此時函數![]() 的單調遞增區間為
的單調遞增區間為![]() 和
和![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
(2)當![]() 時,不等式
時,不等式![]() 即
即 ![]()
令![]() ,
, ![]() 對任意
對任意![]() 恒成立
恒成立
又 ![]()
當![]() 時,
時, ![]() ,所以
,所以![]() 在
在![]() 上遞增,且最小值為
上遞增,且最小值為![]()
(i)當![]() ,即
,即![]() 時,
時, ![]() 對任意
對任意![]() 恒成立
恒成立
![]()
![]() 在
在![]() 上遞增,
上遞增, ![]() 當
當![]() 時,
時, ![]() 滿足題意; (ii)當
滿足題意; (ii)當![]() ,即
,即![]() 時,
時,
由上可得存在唯一的實數![]() ,使得
,使得![]() ,可得當
,可得當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上遞減,此時
上遞減,此時![]() 不符合題意; 綜上得,當
不符合題意; 綜上得,當![]() 時,滿足題意,即符合題意的實數
時,滿足題意,即符合題意的實數![]() 的最大值為
的最大值為![]() .
.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,平面![]() 平面
平面![]() ,且四邊形
,且四邊形![]() 為矩形,四邊形
為矩形,四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
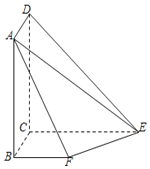
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的大小;
所成銳二面角的大小;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年10月,工信部頒發了國內首個![]() 無線電通信設備進網許可證,標志著
無線電通信設備進網許可證,標志著![]() 基站設備將正式接入公用電信商用網絡.某
基站設備將正式接入公用電信商用網絡.某![]() 手機生產商擬升級設備生產
手機生產商擬升級設備生產![]() 手機,有兩種方案可供選擇,方案1:直接引進
手機,有兩種方案可供選擇,方案1:直接引進![]() 手機生產設備;方案2:對已有的
手機生產設備;方案2:對已有的![]() 手機生產設備進行技術改造,升級到
手機生產設備進行技術改造,升級到![]() 手機生產設備.該生產商對未來
手機生產設備.該生產商對未來![]() 手機銷售市場行情及回報率進行大數據模擬,得到如下統計表:
手機銷售市場行情及回報率進行大數據模擬,得到如下統計表:
市場銷售狀態 | 暢銷 | 平銷 | 滯銷 | |
市場銷售狀態概率 |
|
|
| |
預期年利潤數值(單位:億元) | 方案1 | 70 | 40 | -40 |
方案2 | 60 | 30 | -10 | |
(1)以預期年利潤的期望值為依據,求![]() 的取值范圍,討論該生產商應該選擇哪種方案進行設備升級?
的取值范圍,討論該生產商應該選擇哪種方案進行設備升級?
(2)設該生產商升級設備后生產的![]()
![]() 萬部,通過大數據模擬核算,選擇方案1所生產的
萬部,通過大數據模擬核算,選擇方案1所生產的![]() 手機年度總成本
手機年度總成本![]() (億元),選擇方案2所生產的
(億元),選擇方案2所生產的![]() 手機年度總成為
手機年度總成為![]() (億元).已知
(億元).已知![]() ,當所生產的
,當所生產的![]() 手機市場行情為暢銷、平銷和滯銷時,每部手機銷售單價分別為0.8萬元,
手機市場行情為暢銷、平銷和滯銷時,每部手機銷售單價分別為0.8萬元,![]() (萬元),
(萬元),![]() (萬元),根據(1)的決策,求該生產商所生產的
(萬元),根據(1)的決策,求該生產商所生產的![]() 手機年利潤期望的最大值?并判斷這個年利潤期望的最大值能否達到預期年利潤數值.
手機年利潤期望的最大值?并判斷這個年利潤期望的最大值能否達到預期年利潤數值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度,再把所得的函數圖象上所有點的橫坐標縮短到原來的
個單位長度,再把所得的函數圖象上所有點的橫坐標縮短到原來的![]() (縱坐標不變)得到函數
(縱坐標不變)得到函數![]() 的圖象,關于
的圖象,關于![]() 的說法有:①函數
的說法有:①函數![]() 的圖象關于點
的圖象關于點![]() 對稱;②函數
對稱;②函數![]() 的圖象的一條對稱軸是
的圖象的一條對稱軸是![]() ;③函數
;③函數![]() 在
在![]() 上的最上的最小值為
上的最上的最小值為![]() ;④函數
;④函數![]() 上單調遞增,則以上說法正確的個數是( )
上單調遞增,則以上說法正確的個數是( )
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線C的方程為
中,曲線C的方程為![]() ,以原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
,以原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為![]() .
.
(1)求直線l的直角坐標方程;
(2)已知P是曲線C上的一動點,過點P作直線![]() 交直線于點A,且直線
交直線于點A,且直線![]() 與直線l的夾角為45°,若
與直線l的夾角為45°,若![]() 的最大值為6,求a的值.
的最大值為6,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱錐P﹣ABC中.AB⊥BC,△PAC為等邊三角形,二面角P﹣AC﹣B的余弦值為![]() ,當三棱錐的體積最大時,其外接球的表面積為8π.則三棱錐體積的最大值為( )
,當三棱錐的體積最大時,其外接球的表面積為8π.則三棱錐體積的最大值為( )
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 過點
過點![]() ,傾斜角為
,傾斜角為![]() .以原點為極點,
.以原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程
的極坐標方程![]() .
.
(1)寫出直線![]() 的參數方程及曲線
的參數方程及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,
兩點,![]() 為線段
為線段![]() 的中點,且
的中點,且![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com