
【題目】設常數![]() .在平面直角坐標系xOy中,已知點
.在平面直角坐標系xOy中,已知點![]() ,直線l:
,直線l:![]() ,曲線Γ:
,曲線Γ:![]() (
(![]() ,
,![]() ).l與x軸交于點A、與Γ交于點B.P、Q分別是曲線Γ與線段AB上的動點.
).l與x軸交于點A、與Γ交于點B.P、Q分別是曲線Γ與線段AB上的動點.
(1)用t表示點B到點F的距離;
(2)設![]() ,
,![]() ,線段OQ的中點在直線FP上,求△AQP的面積;
,線段OQ的中點在直線FP上,求△AQP的面積;
(3)設![]() ,是否存在以FP、FQ為鄰邊的矩形FPEQ,使得點E在Γ上?若存在,求點P的坐標;若不存在,說明理由.
,是否存在以FP、FQ為鄰邊的矩形FPEQ,使得點E在Γ上?若存在,求點P的坐標;若不存在,說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)方法一:設B點坐標,根據兩點之間的距離公式,即可求得|BF|;
方法二:根據拋物線的定義,即可求得|BF|;
(2)根據拋物線的性質,求得Q點坐標,即可求得OD的中點坐標,即可求得直線PF的方程,代入拋物線方程,即可求得P點坐標,即可求得△AQP的面積;
(3)設P及E點坐標,根據直線kPFkFQ=﹣1,求得直線QF的方程,求得Q點坐標,根據![]() ,求得E點坐標,則(
,求得E點坐標,則(![]() )2=8(
)2=8(![]() 6),即可求得P點坐標.
6),即可求得P點坐標.
(1)方法一:由題意可知:設![]() ,
,
則![]() ,
,![]() ;
;
方法二:由題意可知:設![]() ,
,
由拋物線的性質可知:![]() ,
,![]() ;
;
(2)![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,
![]() ,
,![]() ,設OQ的中點D,
,設OQ的中點D,![]() ,
,
 ,則直線PF方程:
,則直線PF方程:![]() ,
,
聯立![]() ,整理得:
,整理得:![]() ,解得:
,解得:![]() ,
,![]() (舍去),
(舍去),
![]() △AQP的面積
△AQP的面積![]() ;
;
(3)存在,設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
直線QF方程為![]() ,
,
![]() ,
,![]() ,
,
根據![]() ,則
,則![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 存在以FP、FQ為鄰邊的矩形FPEQ,使得點E在Γ上,且
存在以FP、FQ為鄰邊的矩形FPEQ,使得點E在Γ上,且![]() .
.


科目:高中數學 來源: 題型:
【題目】為了解春季晝夜溫差大小與某種子發芽多少之間的關系,現在從4月份的30天中隨機挑選了5天進行研究,且分別記錄了每天晝夜溫差與每100顆種子浸泡后的發芽數,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
溫差x/oC | 10 | 11 | 13 | 12 | 8 |
發芽數y/顆 | 23 | 25 | 30 | 26 | 16 |
(Ⅰ)從這5天中任選2天,若選取的是4月1日與4月30日的兩組數據,請根據這5天中的另3天的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]()
(Ⅱ)若由線性回歸方程得到的估計數據與所選出的兩組檢驗數據的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得的線性回歸方程是否可靠.
(參考公式, 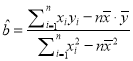 ,
, ![]() ),參考數據
),參考數據![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義![]() ,
,![]() ,…,
,…,![]() 的“倒平均數”為
的“倒平均數”為![]() .
.
(1)若數列![]() 前
前![]() 項的“倒平均數”為
項的“倒平均數”為![]() ,求
,求![]() 的通項公式;
的通項公式;
(2)設數列![]() 滿足:當
滿足:當![]() 為奇數時,
為奇數時,![]() ,當
,當![]() 為偶數時,
為偶數時,![]() .若
.若![]() 為
為![]() 前
前![]() 項的倒平均數,求
項的倒平均數,求![]() ;
;
(3)設函數![]() ,對(1)中的數列
,對(1)中的數列![]() ,是否存在實數
,是否存在實數![]() ,使得當
,使得當![]() 時,
時,![]() 對任意
對任意![]() 恒成立?若存在,求出最大的實數
恒成立?若存在,求出最大的實數![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,
,![]() 為左焦點,
為左焦點,![]() 為上頂點,
為上頂點,![]() 為右頂點,若
為右頂點,若![]() ,拋物線
,拋物線![]() 的頂點在坐標原點,焦點為
的頂點在坐標原點,焦點為![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)是否存在過![]() 點的直線,與
點的直線,與![]() 和
和![]() 交點分別是
交點分別是![]() 和
和![]() ,使得
,使得![]() ?如果存在,求出直線的方程;如果不存在,請說明理由.
?如果存在,求出直線的方程;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于集合A,定義了一種運算“![]() ”,使得集合A中的元素間滿足條件:如果存在元素
”,使得集合A中的元素間滿足條件:如果存在元素![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,則稱元素e是集合A對運算“
,則稱元素e是集合A對運算“![]() ”的單位元素.例如:
”的單位元素.例如:![]() ,運算“
,運算“![]() ”為普通乘法;存在
”為普通乘法;存在![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,所以元素1是集合R對普通乘法的單位元素.下面給出三個集合及相應的運算“
,所以元素1是集合R對普通乘法的單位元素.下面給出三個集合及相應的運算“![]() ”:
”:
①![]() ,運算“
,運算“![]() ”為普通減法;
”為普通減法;
②![]() ,運算“
,運算“![]() ”為矩陣加法;
”為矩陣加法;
③![]() (其中M是任意非空集合),運算“
(其中M是任意非空集合),運算“![]() ”為求兩個集合的交集.
”為求兩個集合的交集.
其中對運算“![]() ”有單位元素的集合序號為( )
”有單位元素的集合序號為( )
A. ①②B. ①③C. ①②③D. ②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,從流水線上隨機抽取100件產品,統計其質量指標值并繪制頻率分布直方圖(如圖):
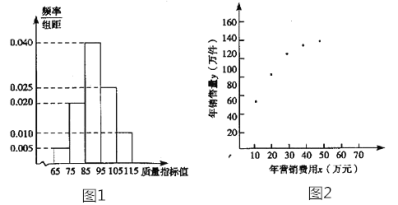
規定產品的質量指標值在![]() 的為劣質品,在
的為劣質品,在![]() 的為優等品,在
的為優等品,在![]() 的為特優品,銷售時劣質品每件虧損1元,優等品每件盈利3元,特優品每件盈利5元.以這100 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
的為特優品,銷售時劣質品每件虧損1元,優等品每件盈利3元,特優品每件盈利5元.以這100 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
(1)求每件產品的平均銷售利潤;
(2)該企業為了解年營銷費用![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:萬件)的影響,對近5年年營銷費用
(單位:萬件)的影響,對近5年年營銷費用![]() 和年銷售量
和年銷售量![]() 數據做了初步處理,得到如圖的散點圖及一些統計量的值.
數據做了初步處理,得到如圖的散點圖及一些統計量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根據散點圖判斷,![]() 可以作為年銷售量
可以作為年銷售量![]() (萬件)關于年營銷費用
(萬件)關于年營銷費用![]() (萬元)的回歸方程.
(萬元)的回歸方程.
①求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
⑦用所求的回歸方程估計該企業應投人多少年營銷費,才能使得該企業的年收益的預報值達到最大?(收益=銷售利潤營銷費用,取![]() )
)
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() 其回歸直線
其回歸直線![]() 均斜率和截距的最小二乘估計分別為
均斜率和截距的最小二乘估計分別為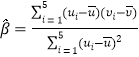 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著中國教育改革的不斷深入,越來越多的教育問題不斷涌現.“衡水中學模式”入駐浙江,可以說是應試教育與素質教育的強烈碰撞.這一事件引起了廣大市民的密切關注.為了了解廣大市民關注教育問題與性別是否有關,記者在北京,上海,深圳隨機調查了100位市民,其中男性55位,女性45位.男性中有45位關注教育問題,其余的不關注教育問題;女性中有30位關注教育問題,其余的不關注教育問題.
(1)根據以上數據完成下列2×2列聯表;
關注教育問題 | 不關注教育問題 | 合計 | |||||
女 | 30 | 45 | |||||
男 | 45 | 55 | |||||
合計 |
| 100 | |||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | ||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | ||
(2)能否在犯錯誤的概率不超過0.025的前提下認為是否關注教育與性別有關系?
參考公式: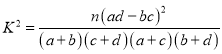 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 經過點
經過點![]() ,左、右焦點分別是
,左、右焦點分別是![]() ,
,![]() ,
,![]() 點在橢圓上,且滿足
點在橢圓上,且滿足![]() 的
的![]() 點只有兩個.
點只有兩個.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過![]() 且不垂直于坐標軸的直線
且不垂直于坐標軸的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,在
兩點,在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使得
,使得![]() 的角平分線是
的角平分線是![]() 軸?若存在求出
軸?若存在求出![]() ,若不存在,說明理由.
,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com