【題目】已知拋物線
（
是正常數）上有兩點
、
，焦點
，
甲：
；
乙：
；
丙：
；
丁：
.
以上是“直線
經過焦點”的充要條件有幾個（ ）
A.
B.
C.
D.
【答案】B
【解析】
設直線
的方程為
，將直線的方程與拋物線的方程聯立，利用韋達定理驗證四個選項結論成立時，實數
的值，可以得出“直線經過焦點
”的充要條件的個數.
設直線的方程為，則直線交
軸于點
，且拋物線的焦點的坐標為
.
將直線的方程與拋物線的方程聯立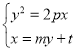
，消去得，
，
由韋達定理得
，
.
對于甲條件，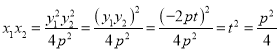
，得
，
甲條件是“直線經過焦點”的必要不充分條件；
對于乙條件，
，得
，此時，直線過拋物線的焦點，
乙條件是“直線經過焦點”的充要條件；
對于丙條件，
，即
，
解得或
，所以，丙條件是“直線經過焦點”的必要不充分條件；
對于丁條件，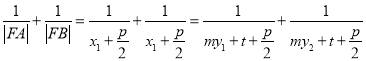
，
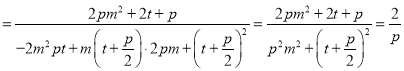化簡得
，得，所以，丁條件是“直線經過焦點”的必要不充分條件.
綜上所述，正確的結論只有
個，故選：B.
全能測控期末小狀元系列答案科目：高中數學 來源： 題型：
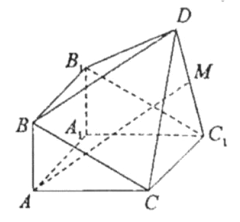
【題目】如圖，由直三棱柱
和四棱錐
構成的幾何體中，
，平面
平面
（I）求證：
；
（II）若M為
中點，求證：
平面
；
（III）在線段BC上（含端點）是否存在點P，使直線DP與平面所成的角為
？若存在，求
得值，若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中超足球隊的后衛線上一共有7名球員，其中3人只能打中后衛，2人只能打邊后衛，2人既能打中后衛又能打邊后衛，主教練決定選派4名后衛上場比賽，假設可以隨機選派球員．
（1）在選派的4人中至少有2人能打邊后衛的概率；
（2）在選派的4人中既能打中后衛又能打邊后衛的人數
的分布列與期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“珠算之父”程大為是我國明代偉大數學家，他的應用數學巨著《算法統綜》的問世，標志著我國的算法由籌算到珠算轉變的完成，程大位在《算法統綜》中常以詩歌的形式呈現數學問題，其中有一首“竹筒容米”問題：“家有九節竹一莖，為因盛米不均平，下頭三節三升九，上稍四節儲三升，唯有中間兩節竹，要將米數次第盛，若有先生能算法，也教算得到天明”（（注）三升九：
升，次第盛；盛米容積依次相差同一數量.）用你所學的數學知識求得中間兩節的容積為（ ）
A.
升B.
升C.
升D.
升
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圖甲中的兩條曲線分別表示某理想狀態下捕食者和被捕食者數量隨時間的變化規律、對捕食者和被捕食者數量之間的關系描述錯誤的是（ ）
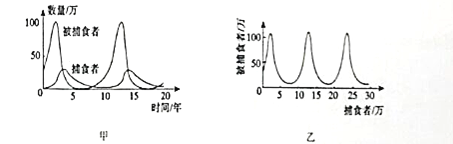
A. 捕食者和被捕食者數量與時間以
年為周期
B. 由圖可知，當捕食者數量增多的過程中，被捕食者數量先增多后減少
C. 捕食者和被捕食者數量之間的關系可以用圖1乙描述
D. 捕食者的數量在第
年和
年之間數量在急速減少
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
