
【題目】已知函數f(x)=﹣x3+ax2+bx+c圖像上的點P(1,f(1))處的切線方程為y=﹣3x+1.
(1)若函數f(x)在x=﹣2時有極值,求f(x)的表達式;
(2)函數f(x)在區間[﹣2,0]上單調遞增,求實數b的取值范圍.
【答案】
(1)解:f′(x)=﹣3x2+2ax+b,
函數f(x)在x=1處的切線斜率為﹣3,
∴f′(1)=﹣3+2a+b=﹣3,即2a+b=0,
又f(1)=﹣1+a+b+c=﹣2得a+b+c=﹣1.
∵函數f(x)在x=﹣2時有極值,
∴f′(﹣2)=﹣12﹣4a+b=0,
聯立 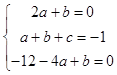 ,
,
解得a=﹣2,b=4,c=﹣3,
∴f(x)=﹣x3﹣2x2+4x﹣3
(2)解:∵函數f(x)在區間[﹣2,0]上單調遞增,
∴導函數f′(x)=﹣3x2﹣bx+b在區間[﹣2,0]上的值恒大于或等于零,
則 ![]() ,
,
解得b≥4,
∴實數b的取值范圍為[4,+∞)
【解析】(1)f′(x)=﹣3x2+2ax+b,由函數f(x)在x=1處的切線斜率為﹣3,可得f′(1)=﹣3;又f(1)=﹣1+a+b+c=﹣2;由函數f(x)在x=﹣2時有極值,可得f′(﹣2)=0,聯立解得即可.(2)由于函數f(x)在區間[﹣2,0]上單調遞增,可得導函數f′(x)=﹣3x2﹣bx+b在區間[﹣2,0]上的值恒大于或等于零,因此 ![]() ,解得即可.
,解得即可.
【考點精析】根據題目的已知條件,利用函數的極值與導數的相關知識可以得到問題的答案,需要掌握求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值.
是極小值.


 課課優能力培優100分系列答案
課課優能力培優100分系列答案 優百分課時互動系列答案
優百分課時互動系列答案科目:高中數學 來源: 題型:
【題目】如圖,某商業中心O有通往正東方向和北偏東30方向的兩條街道,某公園P位于商業中心北偏東![]() 角(
角(![]() ),且與商業中心O的距離為
),且與商業中心O的距離為![]() 公里處,現要經過公園P修一條直路分別與兩條街道交匯于A,B兩處。
公里處,現要經過公園P修一條直路分別與兩條街道交匯于A,B兩處。

(1)當AB沿正北方向時,試求商業中心到A,B兩處的距離和;
(2)若要使商業中心O到A,B兩處的距離和最短,請確定A,B的最佳位置。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某租賃公司擁有汽車100輛.當每輛車的月租金為3000元時,可全部租出.當每輛車的月租金每增加50元時,未租出的車將會增加一輛.租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元.
(1)當每輛車的月租金定為3600元時,能租出多少輛車?
(2)當每輛車的月租金定為多少元時,租賃公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過隨機詢問110名性別不同的大學生是否愛好某項運動,得到如下的列聯表:
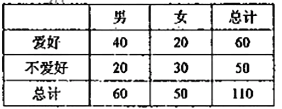
由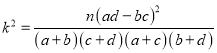 算得,
算得, ![]() .
.
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
則參照附表,得到的正確結論應是( )
A. 在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
B. 在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別無關”
C. 有99%以上的把握認為“愛好該項運動與性別有關”
D. 有99%以上的把握認為“愛好該項運動與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|lgx|﹣( ![]() )x有兩個零點x1 , x2 , 則有( )
)x有兩個零點x1 , x2 , 則有( )
A.x1x2<0
B.x1x2=1
C.x1x2>1
D.0<x1x2<1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=f(x)的圖象如圖所示.觀察圖象可知函數y=f(x)的定義域、值域分別是( )
A.[﹣5,0]∪[2,6),[0,5]
B.[﹣5,6),[0,+∞)
C.[﹣5,0]∪[2,6),[0,+∞)
D.[﹣5,+∞),[2,5]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com