
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.首屆中國國際進口博覽會的某展館棚頂一角的鋼結構可以抽象為空間圖形陽馬.如圖所示,在陽馬![]() 中,
中,![]() 底面
底面![]() .
.
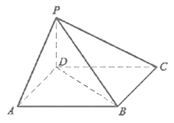
(1)若![]() ,斜梁
,斜梁![]() 與底面
與底面![]() 所成角為
所成角為![]() ,求立柱
,求立柱![]() 的長(精確到
的長(精確到![]() );
);
(2)證明:四面體![]() 為鱉臑;
為鱉臑;
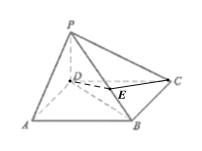
(3)若![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一個動點,求
上一個動點,求![]() 面積的最小值.
面積的最小值.
【答案】(1)![]() ;(2)詳見解析;(3)
;(2)詳見解析;(3)![]() .
.
【解析】
(1)推導出側棱![]() 在平面
在平面![]() 上的射影是
上的射影是![]() ,從而
,從而![]() 是側棱
是側棱![]() 與平面
與平面![]() 所成角,
所成角,![]() ,從而求得立柱
,從而求得立柱![]() 的長.
的長.
(2)四邊形![]() 是長方形,從而
是長方形,從而![]() 是直角三角形,由此得出
是直角三角形,由此得出![]() ,從而三角形
,從而三角形![]() 是直角三角形,由
是直角三角形,由![]() 平面
平面![]() ,得
,得![]() 是直角三角形,由此能證明四面體
是直角三角形,由此能證明四面體![]() 為鱉臑.
為鱉臑.
(3)利用轉化法求出異面直線![]() 與
與![]() 的距離,即可求得三角形
的距離,即可求得三角形![]() 面積的最小值.
面積的最小值.
(1)因為側棱![]() 平面
平面![]() ,所以側棱
,所以側棱![]() 在底面
在底面![]() 上的射影是
上的射影是![]() ,所以
,所以![]() 是側棱
是側棱![]() 與平面
與平面![]() 所成角,所以
所成角,所以![]() ,在
,在![]() 中,
中,![]() ,所以
,所以![]() ,即
,即![]() ,
,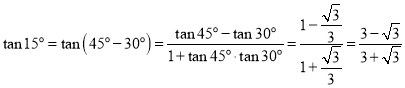 ,所以
,所以![]() .
.
(2)證明:由題意知四邊形![]() 是長方形,所以三角形
是長方形,所以三角形![]() 是直角三角形.
是直角三角形.
由于![]() 平面
平面![]() ,所以
,所以![]() ,所以三角形
,所以三角形![]() 和三角形
和三角形![]() 是直角三角形.因為
是直角三角形.因為![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,所以三角形
,所以三角形![]() 是直角三角形.所以四面體
是直角三角形.所以四面體![]() 為鱉臑.
為鱉臑.
(3)![]() 與
與![]() 是兩異面直線,
是兩異面直線,![]() ,所以
,所以![]() 平面
平面![]() ,則兩異面直線
,則兩異面直線![]() 與
與![]() 的距離等于
的距離等于![]() 到平面
到平面![]() 的距離,也即
的距離,也即![]() 到平面
到平面![]() 的距離,等于
的距離,等于![]() 到直線
到直線![]() 的距離.因為
的距離.因為![]() ,所以
,所以![]() ,則
,則![]() 到
到![]() 的距離為
的距離為![]() .
.
所以線段![]() 上的動點
上的動點![]() 到
到![]() 的最小距離為
的最小距離為![]() .則三角形
.則三角形![]() 面積的最小值為
面積的最小值為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】設![]() ,為正項數(shù)列
,為正項數(shù)列![]() 的前n項和,且
的前n項和,且![]() .數(shù)列
.數(shù)列![]() 滿足:
滿足:![]() ,
,![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)設![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() ,其長軸、焦距和短軸的長的平方依次成等差數(shù)列
,其長軸、焦距和短軸的長的平方依次成等差數(shù)列![]() 直線l與x軸正半軸和y軸分別交于點Q、P,與橢圓分別交于點M、N,各點均不重合且滿足
直線l與x軸正半軸和y軸分別交于點Q、P,與橢圓分別交于點M、N,各點均不重合且滿足![]() .
.
![]() 求橢圓的標準方程;
求橢圓的標準方程;
![]() 若
若![]() ,試證明:直線l過定點并求此定點.
,試證明:直線l過定點并求此定點.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓C1:![]() y2=1的左右頂點是雙曲線C2:
y2=1的左右頂點是雙曲線C2:![]() 的頂點,且橢圓C1的上頂點到雙曲線C2的漸近線的距離為
的頂點,且橢圓C1的上頂點到雙曲線C2的漸近線的距離為![]() .
.
(1)求雙曲線C2的方程;
(2)若直線與C1相交于M1,M2兩點,與C2相交于Q1,Q2兩點,且![]()
![]() 5,求|M1M2|的取值范圍.
5,求|M1M2|的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖(一),在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,將
的中點,將![]() 沿
沿![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置得到圖(二),點
的位置得到圖(二),點![]() 為棱
為棱![]() 上的動點.
上的動點.

(1)當![]() 在何處時,平面
在何處時,平面![]() 平面
平面![]() ,并證明;
,并證明;
(2)若![]() ,
,![]() ,證明:點
,證明:點![]() 到平面
到平面![]() 的距離等于點
的距離等于點![]() 到平面
到平面![]() 的距離,并求出該距離.
的距離,并求出該距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
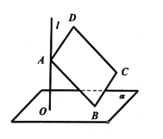
【題目】已知直線![]() ⊥平面
⊥平面![]() 垂足為
垂足為![]() 在矩形ABCD中,AD=1,AB=2,若點A在
在矩形ABCD中,AD=1,AB=2,若點A在![]() 上移動,點B在平面
上移動,點B在平面![]() 上移動,則
上移動,則![]() D兩點間的最大距離為_______.
D兩點間的最大距離為_______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓O經過橢圓C:![]() =1(a>b>0)的兩個焦點以及兩個頂點,且點(b,
=1(a>b>0)的兩個焦點以及兩個頂點,且點(b,![]() )在橢圓C上.
)在橢圓C上.
(Ⅰ)求橢圓C的方程;
(Ⅱ)若直線l與圓O相切,與橢圓C交于M、N兩點,且|MN|=![]() ,求直線l的傾斜角.
,求直線l的傾斜角.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com