
【題目】設函數![]() ,則下列結論正確的是__________.(寫出所有正確的編號)①
,則下列結論正確的是__________.(寫出所有正確的編號)①![]() 的最小正周期為
的最小正周期為![]() ;②
;②![]() 在區間
在區間![]() 上單調遞增;③
上單調遞增;③![]() 取得最大值的
取得最大值的![]() 的集合為
的集合為![]() ④將
④將![]() 的圖像向左平移
的圖像向左平移![]() 個單位,得到一個奇函數的圖像
個單位,得到一個奇函數的圖像
 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 的定義域;
的定義域;
(2)判斷![]() 的奇偶性;
的奇偶性;
(3)方程![]() 是否有實根?如果有實根
是否有實根?如果有實根![]() ,請求出一個長度為
,請求出一個長度為![]() 的區間
的區間![]() ,使
,使![]() ;如果沒有,請說明理由(注:區間
;如果沒有,請說明理由(注:區間![]() 的長度
的長度![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠某種產品的年固定成本為250萬元,每生產![]() 件,需另投入成本
件,需另投入成本![]() ,當年產量不足80件時,
,當年產量不足80件時, ![]() (萬元),當年產量不少于80件時
(萬元),當年產量不少于80件時![]() (萬元),每件商品售價50萬元,通過市場分析,該廠生產的商品能全部售完.
(萬元),每件商品售價50萬元,通過市場分析,該廠生產的商品能全部售完.
(1)寫出年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (件)的函數解析式;
(件)的函數解析式;
(2)年產量為多少件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是一幾何體的平面展開圖,其中四邊形![]() 為正方形,
為正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為全等的等邊三角形,
為全等的等邊三角形, ![]() 分別為
分別為![]() 的中點.在此幾何體中,下列結論中錯誤的為( )
的中點.在此幾何體中,下列結論中錯誤的為( )
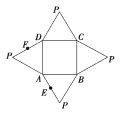
A. 直線![]() 與直線
與直線![]() 共面 B. 直線
共面 B. 直線![]() 與直線
與直線![]() 是異面直線
是異面直線
C. 平面![]() 平面
平面![]() D. 面
D. 面![]() 與面
與面![]() 的交線與
的交線與![]() 平行
平行
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的四邊形ABCD,已知 ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3)
=(﹣2,﹣3)
(1)若 ![]() 且﹣2≤x<1,求函數y=f(x)的值域;
且﹣2≤x<1,求函數y=f(x)的值域;
(2)若 ![]() 且
且 ![]() ,求x,y的值及四邊形ABCD的面積.
,求x,y的值及四邊形ABCD的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的二次函數f(x)=ax2﹣4bx+1.設集合P={1,2,3}和Q={﹣1,1,2,3,4},分別從集合P和Q中隨機取一個數作為a和b,求函數y=f(x)在區間[1,+∞)上是增函數的概率
(1)已知關于x的二次函數f(x)=ax2﹣4bx+1.設集合P={1,2,3}和Q={﹣1,1,2,3,4},分別從集合P和Q中隨機取一個數作為a和b,求函數y=f(x)在區間[1,+∞)上是增函數的概率;
(2)在區間[1,5]和[2,4]上分別取一個數,記為a,b,求方程 ![]() +
+ ![]() =1表示焦點在x軸上且離心率小于
=1表示焦點在x軸上且離心率小于 ![]() 的橢圓的概率.
的橢圓的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間的一臺機床生產出一批零件,現從中抽取8件,將其編為![]() ,
, ![]() ,…,
,…, ![]() ,測量其長度(單位:
,測量其長度(單位: ![]() ),得到下表中數據:
),得到下表中數據:
編號 |
|
|
|
|
|
|
|
|
長度 | 1.49 | 1.46 | 1.51 | 1.51 | 1.53 | 1.51 | 1.47 | 1.51 |
其中長度在區間![]() 內的零件為一等品.
內的零件為一等品.
(1)從上述8個零件中,隨機抽取一個,求這個零件為一等品的概率;
(2)從一等品零件中,隨機抽取2個.
①用零件的編號列出所有可能的抽取結果;
②求這2個零件長度相等的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究所計劃利用“神十”宇宙飛船進行新產品搭載實驗,計劃搭載若干件新產品A、B,該所要根據該產品的研制成本、產品重量、搭載實驗費用和預計產生的收益來決定具體搭載安排,有關數據如表:
每件產品A | 每件產品B | ||
研制成本、搭載 | 20 | 30 | 計劃最大資金額 |
產品重量(千克) | 10 | 5 | 最大搭載重量110千克 |
預計收益(萬元) | 80 | 60 |
分別用x,y表示搭載新產品A,B的件數.總收益用Z表示
(Ⅰ)用x,y列出滿足生產條件的數學關系式,并畫出相應的平面區域;
(Ⅱ)問分別搭載新產品A、B各多少件,才能使總預計收益達到最大?并求出此最大收益.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com