
【題目】設![]() 為奇函數,
為奇函數,![]() 為實常數.
為實常數.
(1)求![]() 的值;
的值;
(2)證明:![]() 在區間
在區間![]() 內單調遞增;
內單調遞增;
(3)若對于區間![]() 上的每一個
上的每一個![]() 的值,不等式
的值,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 滿足
滿足![]() ,且
,且![]() 的最小值是
的最小值是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有唯一實數根,求實數
上有唯一實數根,求實數![]() 的取值范圍;
的取值范圍;
(3)函數![]() ,對任意
,對任意![]() 都有
都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)滿足:對于s,t∈[0,+∞),都有f(s)≥0,f(t)≥0,且f(s)+f(t)≤f(s+t),則稱函數f (x)為“T函數”.
(I)試判斷函數f1(x)=x2與f2(x)=lg(x+1)是否是“T函數”,并說明理由;
(Ⅱ)設f (x)為“T函數”,且存在x0∈[0,+∞),使f(f(x0))=x0.求證:f (x0) =x0;
(Ⅲ)試寫出一個“T函數”f(x),滿足f(1)=1,且使集合{y|y=f(x),0≤x≤1)中元素的個數最少.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題p:關于x的方程x2+ax+2=0無實根,命題q:函數f(x)=logax在(0,+∞)上單調遞增,若“p∧q”為假命題,“p∨q”真命題,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F1 , F2分別是C: ![]() +
+ ![]() =1(a>b>0)的左,右焦點,M是C上一點且MF2與x軸垂直,直線MF1與C的另一個交點為N.
=1(a>b>0)的左,右焦點,M是C上一點且MF2與x軸垂直,直線MF1與C的另一個交點為N.
(1)若直線MN的斜率為 ![]() ,求C的離心率;
,求C的離心率;
(2)若直線MN在y軸上的截距為2,且|MN|=5|F1N|,求a,b.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 對任意實數
對任意實數![]() 均有
均有![]() ,其中常數
,其中常數![]() 為負數,且
為負數,且![]() 在區間
在區間![]() 上有表達式
上有表達式![]() .
.
(1)寫出![]() 在
在![]() 上的表達式,并寫出函數
上的表達式,并寫出函數![]() 在
在![]() 上的單調區間(不用過程,直接寫出即可);
上的單調區間(不用過程,直接寫出即可);
(2)求出![]() 在
在![]() 上的最小值與最大值,并求出相應的自變量的取值.
上的最小值與最大值,并求出相應的自變量的取值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,則下列結論正確的是__________.(寫出所有正確的編號)①
,則下列結論正確的是__________.(寫出所有正確的編號)①![]() 的最小正周期為
的最小正周期為![]() ;②
;②![]() 在區間
在區間![]() 上單調遞增;③
上單調遞增;③![]() 取得最大值的
取得最大值的![]() 的集合為
的集合為![]() ④將
④將![]() 的圖像向左平移
的圖像向左平移![]() 個單位,得到一個奇函數的圖像
個單位,得到一個奇函數的圖像
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 年初的時候,國家政府工作報告明確提出,
年初的時候,國家政府工作報告明確提出, ![]() 年要堅決打好藍天保衛戰,加快解決燃煤污染問題,全面實施散煤綜合治理.實施煤改電工程后,某縣城的近六個月的月用煤量逐漸減少,
年要堅決打好藍天保衛戰,加快解決燃煤污染問題,全面實施散煤綜合治理.實施煤改電工程后,某縣城的近六個月的月用煤量逐漸減少, ![]() 月至
月至![]() 月的用煤量如下表所示:
月的用煤量如下表所示:
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
(1)由于某些原因, ![]() 中一個數據丟失,但根據
中一個數據丟失,但根據![]() 至
至![]() 月份的數據得出
月份的數據得出![]() 樣本平均值是
樣本平均值是![]() ,求出丟失的數據;
,求出丟失的數據;
(2)請根據![]() 至
至![]() 月份的數據,求出
月份的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)現在用(2)中得到的線性回歸方程中得到的估計數據與![]() 月
月![]() 月的實際數據的誤差來判斷該地區的改造項目是否達到預期,若誤差均不超過
月的實際數據的誤差來判斷該地區的改造項目是否達到預期,若誤差均不超過![]() ,則認為該地區的改造已經達到預期,否則認為改造未達預期,請判斷該地區的煤改電項目是否達預期?
,則認為該地區的改造已經達到預期,否則認為改造未達預期,請判斷該地區的煤改電項目是否達預期?
(參考公式:線性回歸方程![]() ,其中
,其中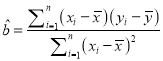
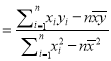 )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com