【題目】已知實數x，y滿足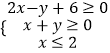 
，若目標函數z=﹣mx+y的最大值為﹣2m+10，最小值為﹣2m﹣2，則實數m的取值范圍是（ ）
A.[﹣1，2]
B.[﹣2，1]
C.[2，3]
D.[﹣1，3]
【答案】A
【解析】解：作出不等式組對應的平面區域如圖：（陰影部分ABC）． 由目標函數z=﹣mx+y得y=mx+z，
則直線的截距最大，z最大，直線的截距最小，z最小．
∵目標函數z=﹣mx+y的最大值為﹣2m+10，最小值為﹣2m﹣2，
∴當目標函數經過點（2，10）時，取得最大，
當經過點（2，﹣2）時，取得最小值，
∴目標函數z=﹣mx+y的目標函數的斜率m滿足比x+y=0的斜率大，比2x﹣y+6=0的斜率小，
即﹣1≤m≤2，
故選：A．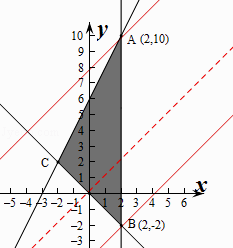
作出不等式組對應的平面區域，利用目標函數的幾何意義，由z=﹣mx+y的最大值為﹣2m+10，即當目標函數經過點（2，10）時，取得最大，當經過點（2，﹣2）時，取得最小值，利用數形結合確定m的取值范圍．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知點 
，點P是圓 
上的任意一點，設Q為該圓的圓心，并且線段PA的垂直平分線與直線PQ交于點E．
（1）求點E的軌跡方程；
（2）已知M，N兩點的坐標分別為（﹣2，0），（2，0），點T是直線x=4上的一個動點，且直線TM，TN分別交（1）中點E的軌跡于C，D兩點（M，N，C，D四點互不相同），證明：直線CD恒過一定點，并求出該定點坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知各項都為正數的數列{an}滿足a1=1，an2﹣（2an﹣1﹣1）an﹣2an﹣1=0（n≥2，n∈N*），數列{bn}滿足b1=1，b1+ 
b2+ 
b3+…+ 
bn=bn+1﹣1（n∈N*）
（Ⅰ）求{an}，{bn}的通項公式；
（Ⅱ）求數列{anbn}的前n項和為Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱柱
中， 
平面
， 
， 
， 
， 
， 
為
的中點.
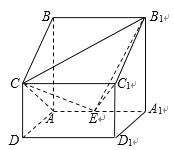
（Ⅰ）求四棱錐
的體積；
（Ⅱ）設點
在線段
上，且直線
與平面
所成角的正弦值為
，求線段
的長度；
（Ⅲ）判斷線段
上是否存在一點
，使得
？（結論不要求證明）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的幾何體，關于其結構特征，下列說法不正確的是
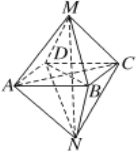
A. 該幾何體是由兩個同底的四棱錐組成的幾何體
B. 該幾何體有12條棱、6個頂點
C. 該幾何體有8個面，并且各面均為三角形
D. 該幾何體有9個面，其中一個面是四邊形，其余均為三角形
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設m, n是兩條不同的直線,
是三個不同的平面, 給出下列四個命題:
①若m⊥α,n∥α,則m⊥n;； ②若α∥β, β∥r, m⊥α,則m⊥r;
③若m∥α,n∥α,則m∥n;； ④若α⊥r, β⊥r,則α∥β．
其中正確命題的序號是 （ ）
A. 
①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
、圓
均滿足圓心在直線
： 
上，過點
，且與直線l2：x=-1相切．
（1）當
時，求圓，圓的標準方程；
（2）直線l2與圓、圓分別相切于A，B兩點，求
的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
sinωx﹣ 
cosωx（ω＞0），將函數y=|f（x）|的圖象向左平移 
個單位長度后關于y軸對稱，則當ω取最小值時，g（x）=cos（ωx+ 
）的單調遞減區間為（ ）
A.[﹣ 
+ 
， 
+ ]（k∈Z）
B.[﹣ + 
， + ]（k∈Z）
C.[﹣ 
+ ， + ]（k∈Z）
D.[﹣ + ， + ]（k∈Z）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某旅游城市為向游客介紹本地的氣溫情況，繪制了一年中各月平均最高氣溫和平均最低氣溫的雷達圖. 圖中A點表示十月的平均最高氣溫約為
，B點表示四月的平均最低氣溫約為
. 下面敘述不正確的是 （ ）
A. 各月的平均最低氣溫都在
以上
B. 七月的平均溫差比一月的平均溫差大
C. 三月和十一月的平均最高氣溫基本相同
D. 平均最高氣溫高于
的月份有5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com