
【題目】已知圓![]() 、圓
、圓![]() 均滿足圓心在直線
均滿足圓心在直線![]() :
: ![]() 上,過點
上,過點![]() ,且與直線l2:x=-1相切.
,且與直線l2:x=-1相切.
(1)當![]() 時,求圓
時,求圓![]() ,圓
,圓![]() 的標準方程;
的標準方程;
(2)直線l2與圓![]() 、圓
、圓![]() 分別相切于A,B兩點,求
分別相切于A,B兩點,求![]() 的最小值.
的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)設出圓的標準方程,圓心為(an,bn),半徑為rm,根據已知條件列方程,解方程即可;
(2)根據圓過(1,0),與x=-1相切,且圓心在直線x-my-2=0上,得方程b2-4mb-8=0,結合圖象,用含m的式子表示出![]() ,進而求出
,進而求出![]() 的最小值。
的最小值。
設圓![]() .
.
依題意得: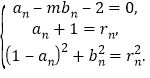
消去![]() 得
得
消去![]() 得
得![]() .
.
(1)當![]() 時,
時,![]() ,解得
,解得![]() 或
或![]() .
.
當![]() 時,
時,![]()
當![]() 時,
時,![]()
所以圓![]() ,圓
,圓![]() 的標準方程分別為:
的標準方程分別為:![]() ,
,![]() .
.
(2)根據題意,如圖:
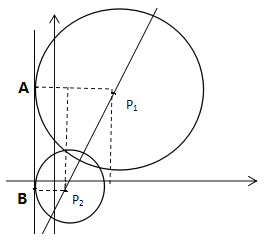
設圓的方程為(x-a)2+(y-b)2=r2,
已知過(1,0),得方程(1-a)2+b2=r2 ① ![]()
已知圓心在直線![]()
![]() 上 ,得方程a-mb-2=0,得a=mb+2 ②,
上 ,得方程a-mb-2=0,得a=mb+2 ②,
已知直線l :x=-1與圓切與A,B,得r=a+1 ③
綜合①②③得b2-4mb-8=0,
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.
故當且僅當![]() 時,
時,![]() 取得最小值
取得最小值![]() .
.


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】已知以點![]() 為圓心的圓經過點
為圓心的圓經過點![]() 和
和![]() ,線段
,線段![]() 的垂直平分線交圓
的垂直平分線交圓![]() 于點
于點![]() 和
和![]() ,且
,且![]() .
.
(1)求直線![]() 的方程;
的方程;
(2)求圓![]() 的方程;
的方程;
(3)設點![]() 在圓
在圓![]() 上,試問使△
上,試問使△![]() 的面積等于8的點
的面積等于8的點![]() 共有幾個?證明你的結論.
共有幾個?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,已知 ![]() cosB+
cosB+ ![]() cosA=
cosA= ![]() (I)求∠C的大小;
(I)求∠C的大小;
(II)求sinB﹣ ![]() sinA的最小值.
sinA的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知實數x,y滿足 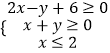 ,若目標函數z=﹣mx+y的最大值為﹣2m+10,最小值為﹣2m﹣2,則實數m的取值范圍是( )
,若目標函數z=﹣mx+y的最大值為﹣2m+10,最小值為﹣2m﹣2,則實數m的取值范圍是( )
A.[﹣1,2]
B.[﹣2,1]
C.[2,3]
D.[﹣1,3]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形, ![]() 是
是![]() 的中點,
的中點, ![]() 是
是![]() 的中點,
的中點, ![]() 是
是![]() 中點.
中點.
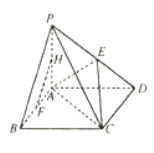
(1)證明: ![]() 平面
平面![]() ;
;
(2)若平面![]() 底面
底面![]() ,
, ![]() ,試在
,試在![]() 上找一點
上找一點![]() ,使
,使![]() 平面
平面![]() ,并證明此結論.
,并證明此結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx+x+ ![]() .
.
(Ⅰ)若a=﹣2,求曲線y=f(x)在點(1,f(1))處的切線方程;
(Ⅱ)若關于x的不等式f(x)≥a+1在(0,+∞)上恒成立,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某險種的基本保費為a(單位:元),繼續購買該險種的投保人稱為續保人,續保人的本年度的保費與其上年度的出險次數的關聯如下:
上年度出險次數 | 0 | 1 | 2 | 3 | 4 |
|
保費 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
設該險種一續保人一年內出險次數與相應概率如下:
一年內出險次數 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0. 05 |
(1)求一續保人本年度的保費高于基本保費的概率;
(2)若一續保人本年度的保費高于基本保費,求其保費比基本保費高出60%的概率;
(3)求續保人本年度的平均保費與基本保費的比值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com