Question

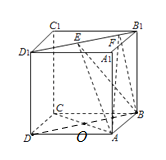
【題目】如圖，正方體棱長為，線段上有兩個動點，且，則下列結論正確的是（ ）

A.平面

B.始終在同一個平面內

C.平面

D.三棱錐的體積為定值

Answer 1

【答案】ACD

【解析】

根據題意，依次如圖可知，連接交于點，則，通過線面垂直的判定定理可證出平面，即可證出平面，可判斷A正確；根據，，，不在一個平面進而斷定B錯誤；由于，根據線面平行的判定，即可判斷出C正確；可分別求得和，且平面，則求出三棱錐的體積，且為定值，即可判斷D項正確.

解：由題可知，正方體棱長為，

則平面，而平面，

，

連接交于點，則，

而，平面，

平面，

由于是線段上的兩個動點，則，

平面，，

又，所以平面，故選項A正確；

，，同在平面上，而不在平面上，

，不在同一個平面內，故選項B錯誤；

，面，面，

平面，故選項C正確；

由于，，且，

，

由于平面，則平面，

，

由于底面積和高都不變，則體積為定值，故選項D正確.

故選：ACD.