
【題目】【2015高考湖北】如圖,圓C與x軸相切于點T(1,0),與y軸正半軸交于兩點A,B(B在A的上方),且|AB|=2.
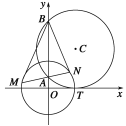
(1)圓C的標準方程為________.
(2)過點A任作一條直線與圓O:x2+y2=1相交于M,N兩點,下列三個結論:
①![]() =
=![]() ;②
;②![]() -
-![]() =2;
=2;
③![]() +
+![]() =2
=2![]() .
.
其中正確結論的序號是________(寫出所有正確結論的序號).
【答案】(1)(x-1)2+(y-![]() )2=2 (2)①②③
)2=2 (2)①②③
【解析】(1)取AB的中點D,連接CD,則CD⊥AB.
由題意|AD|=|CD|=1,
故|AC|=![]() =
=![]() ,即圓C的半徑為
,即圓C的半徑為![]() .
.
又因為圓C與x軸相切于點T(1,0),所以圓心C的坐標為(1,![]() ),故圓C的標準方程為(x-1)2+(y-
),故圓C的標準方程為(x-1)2+(y-![]() )2=2.
)2=2.
(2)在(x-1)2+(y-![]() )2=2中,令x=0,得y=
)2=2中,令x=0,得y=![]() ±1,
±1,
故A(0,![]() -1),B(0,
-1),B(0,![]() +1).設M(x1,y1),N(x2,y2),
+1).設M(x1,y1),N(x2,y2),
當直線MN斜率不存在時,令M(0,-1),N(0,1),
則![]() =
=![]() =
=![]() -1,
-1,![]() =
=![]() =
=![]() -1.
-1.
∴![]() =
=![]() .
.
當直線MN斜率存在時,設直線MN的方程為y=kx+![]() -1,由
-1,由![]()
得(1+k2)x2+2(![]() -1)kx+2(1-
-1)kx+2(1-![]() )=0,
)=0,
則x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
kBM+kNB=![]() +
+![]()
=![]() +
+![]()
=![]() +
+![]() =-
=-![]() +2k
+2k
=-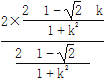 +2k=0,
+2k=0,
所以kBM=-kNB,所以∠MBA=∠NBA,BA是∠MBN的平分線.
由內角平分線定理得![]() =
=![]() ,即
,即![]() =
=![]() .
.
故![]() =
=![]() 恒成立.
恒成立.
當k=0時,可求得![]() =
=![]() -1,
-1,
故![]() =
=![]() -1為定值.
-1為定值.
所以![]() -
-![]() =
=![]() -(
-(![]() -1)=2,
-1)=2,
![]() +
+![]() =
=![]() +
+![]() -1=2
-1=2![]() .
.
故①②③都正確.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:高中數學 來源: 題型:
【題目】過橢圓![]() :
: ![]() 上一點
上一點![]() 向
向![]() 軸作垂線,垂足為右焦點
軸作垂線,垂足為右焦點![]() ,
, ![]() 、
、![]() 分別為橢圓
分別為橢圓![]() 的左頂點和上頂點,且
的左頂點和上頂點,且![]() ,
, ![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若動直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,且以
兩點,且以![]() 為直徑的圓恒過坐標原點
為直徑的圓恒過坐標原點![]() .問是否存在一個定圓與動直線
.問是否存在一個定圓與動直線![]() 總相切.若存在,求出該定圓的方程;若不存在,請說明理由.
總相切.若存在,求出該定圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某志愿者到某山區小學支教,為了解留守兒童的幸福感,該志愿者對某班40名學生進行了一次幸福指數的調查問卷,并用莖葉圖表示如下(注:圖中幸福指數低于70,說明孩子幸福感弱;幸福指數不低于70,說明孩子幸福感強).
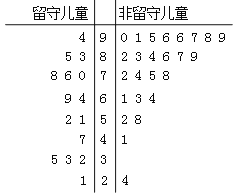
(Ⅰ)根據莖葉圖中的數據完成![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為孩子的幸福感強與是否是留守兒童有關?
的把握認為孩子的幸福感強與是否是留守兒童有關?
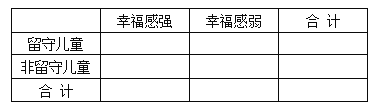
(Ⅱ)從15個留守兒童中按幸福感強弱進行分層抽樣,共抽取5人,又在這5人中隨機抽取2人進行家訪,求這2個學生中恰有一人幸福感強的概率.
參考公式: 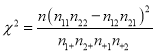 ; 附表:
; 附表:
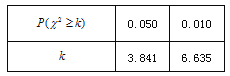
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分圖象如圖所示.
)的部分圖象如圖所示. 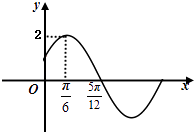
(1)求函數f(x)的解析式;
(2)令g(x)=f(﹣x﹣ ![]() ),求g(x)的單調遞增區間.
),求g(x)的單調遞增區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com