（12分）定義在[-1，1]上的奇函數
當
時，
（Ⅰ）求
在[-1，1]上的解析式；
（Ⅱ）判斷在（0，1）上的單調性，并給予證明.
科目：高中數學 來源： 題型：解答題
（本小題12分）
已知函數f(x)=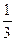
x
－（2a+1）
x
+3a（a+2）x+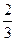
，其中a為實數。
（1）當a=－1時，求函數y=f(x)在[0,6]上的最大值與最小值；
（2）當函數y=f
(x)的圖像在（0,6）上與x軸有唯一的公共點時，求實數a的取值范圍。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分10分）
設f(x)為定義在R上的偶函數，當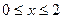
時，y＝x；當x>2時，y＝f(x)的圖像是頂點在P(3,4),且過點A(2,2)的拋物線的一部分
(1)求函數f（x）在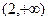
上的解析式；
(2)在下面的直角坐標系中直接畫出函數f（x）的圖像；
(3)寫出函數f(x)值域。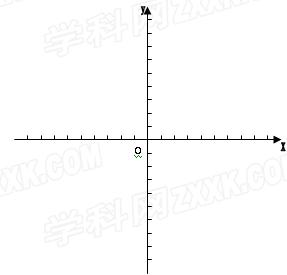
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分） 某校學生社團心理學研究小組在對學生上課注意力集中情況的調查研究中，發現其注意力指數
與聽課時間
之間的關系滿足如圖所示的曲線．當
時，曲線是二次函數圖象的一部分，當
式，曲線是函數
(
且
)圖象的一部分．根據專家研究，當注意力指數大于等于80時聽課效果最佳．
(1) 試求
的函數關系式；
(2) 老師在什么時段內安排核心內容能使得學生聽課效果最佳？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本題滿分14分）
定義在R上的單調函數f(x)滿足f(3)＝log23且對任意x，y∈R都有
f(x+y)＝f (x )+ f(y)．
（Ⅰ）求證f (x)為奇函數；K^S*5U.C#
（Ⅱ）若
，對任意x∈R恒成立，求實數k的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
為奇函數。且
.（1）求實數
的值。
（－1，1）上是增函數。
。
的定義域為集合M，函數
的定義域為集合N．
，
．
函數
的定義域為集合
,
(2)
(3) (
是定義在
上的奇函數，當
時，
，
.