
【題目】已知函數![]()
![]() 的最大值是0,函數
的最大值是0,函數![]()
![]() .
.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)若當![]() 時,不等式
時,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)求出函數的導函數,根據函數的單調性求出f(x)的最大值,得到關于m的方程,進而求出m的值;
(Ⅱ)構造函數F(x)=f(x)-g(x),求出函數的導函數![]() ,進而求出
,進而求出![]() 的導函數
的導函數![]() ,利用導數與函數單調性的關系,通過討論a的范圍,得到函數的單調區間,結合函數恒成立問題,進而求出a的取值范圍.
,利用導數與函數單調性的關系,通過討論a的范圍,得到函數的單調區間,結合函數恒成立問題,進而求出a的取值范圍.
(Ⅰ)函數![]() 的定義域為
的定義域為![]()
![]() ,
,
因為![]() ,所以
,所以![]() 在
在![]() 上單調遞減.
上單調遞減.
令![]() ,得
,得![]()
當![]() 時,
時,![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() 單調遞減;
單調遞減;
所以,當![]() 時,
時,![]() =
=![]()
于是,![]() ,得
,得![]() ,
,
易知,函數![]() 在
在![]() 處有唯一零點,所以
處有唯一零點,所以![]() ,
,![]() .
.
(Ⅱ)令![]() ,
,![]()
則![]() ,
,
設![]()
則![]() ,
,
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,
則![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,
故當![]() 時,
時,![]() ,與已知矛盾.
,與已知矛盾.
②當![]() 時,
時,![]()
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,
則![]() 時,
時,![]()
故![]() 在
在![]() 上單調遞減,
上單調遞減,
則當![]() 時,
時,![]() ,與已知矛盾.
,與已知矛盾.
③當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,
則![]() 時,
時,![]()
所以![]() 在
在![]() 上單調遞增,故當
上單調遞增,故當![]() 時,
時,![]() 恒成立.
恒成立.
綜上,實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】一個經銷鮮花產品的微店,為保障售出的百合花品質,每天從云南鮮花基地空運固定數量的百合花,如有剩余則免費分贈給第二天購花顧客,如果不足,則從本地鮮花供應商處進貨.今年四月前10天,微店百合花的售價為每支2元,云南空運來的百合花每支進價1.6元,本地供應商處百合花每支進價1.8元,微店這10天的訂單中百合花的需求量(單位:支)依次為:251,255,231,243,263,241,265,255,244,252.
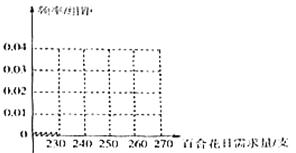
(Ⅰ)求今年四月前10天訂單中百合花需求量的平均數和眾數,并完成頻率分布直方圖;
(Ⅱ)預計四月的后20天,訂單中百合花需求量的頻率分布與四月前10天相同,百合花進貨價格與售價均不變,請根據(Ⅰ)中頻率分布直方圖判斷(同一組中的需求量數據用該組區間的中點值作代表,位于各區間的頻率代替位于該區間的概率),微店每天從云南固定空運250支,還是255支百合花,四月后20天百合花銷售總利潤會更大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設曲線![]() (a為正常數)與
(a為正常數)與![]() 在x軸上方僅有一個公共點P.
在x軸上方僅有一個公共點P.
(1)求實數m的取值范圍(用a表示);
(2)O為原點,若![]() 與x軸的負半軸交于點A,當
與x軸的負半軸交于點A,當![]() 時,試求△OAP的面積的最大值(用a表示).
時,試求△OAP的面積的最大值(用a表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在古裝電視劇《知否》中,甲乙兩人進行一種投壺比賽,比賽投中得分情況分“有初”“貫耳”“散射”“雙耳”“依竿”五種,其中“有初”算“兩籌”,“貫耳”算“四籌”,“散射”算“五籌”,“雙耳”算“六籌”,“依竿”算“十籌”,三場比賽得籌數最多者獲勝.假設甲投中“有初”的概率為![]() ,投中“貫耳”的概率為
,投中“貫耳”的概率為![]() ,投中“散射”的概率為
,投中“散射”的概率為![]() ,投中“雙耳”的概率為
,投中“雙耳”的概率為![]() ,投中“依竿”的概率為
,投中“依竿”的概率為![]() ,乙的投擲水平與甲相同,且甲乙投擲相互獨立.比賽第一場,兩人平局;第二場,甲投了個“貫耳”,乙投了個“雙耳”,則三場比賽結束時,甲獲勝的概率為( )
,乙的投擲水平與甲相同,且甲乙投擲相互獨立.比賽第一場,兩人平局;第二場,甲投了個“貫耳”,乙投了個“雙耳”,則三場比賽結束時,甲獲勝的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年12月以來,湖北省武漢市持續開展流感及相關疾病監測,發現多起病毒性肺炎病例,均診斷為病毒性肺炎/肺部感染,后被命名為新型冠狀病毒肺炎(CoronaVirusDisease2019,COVID—19),簡稱“新冠肺炎”.下圖是2020年1月15日至1月24日累計確診人數隨時間變化的散點圖.
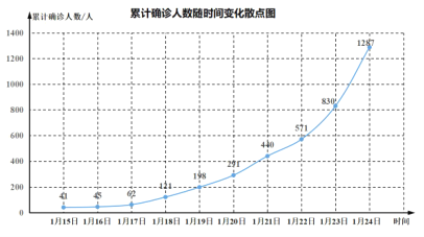
為了預測在未釆取強力措施下,后期的累計確診人數,建立了累計確診人數y與時間變量t的兩個回歸模型,根據1月15日至1月24日的數據(時間變量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根據散點圖判斷,![]() 與
與![]() 哪一個適宜作為累計確診人數y與時間變量t的回歸方程類型?(給出判斷即可,不必說明理由)
哪一個適宜作為累計確診人數y與時間變量t的回歸方程類型?(給出判斷即可,不必說明理由)
(2根據(1)的判斷結果及附表中數據,建立y關于x的回歸方程;
(3)以下是1月25日至1月29日累計確診人數的真實數據,根據(2)的結果回答下列問題:
時間 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累計確診人數的真實數據 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)當1月25日至1月27日這3天的誤差(模型預測數據與真實數據差值的絕對值與真實數據的比值)都小于0.1則認為模型可靠,請判斷(2)的回歸方程是否可靠?
(ⅱ)2020年1月24日在人民政府的強力領導下,全國人民共同采取了強力的預防“新冠肺炎”的措施,若采取措施5天后,真實數據明顯低于預測數據,則認為防護措施有效,請判斷預防措施是否有效?
附:對于一組數據(![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為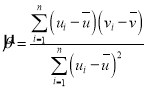 ,
,![]() .
.
參考數據:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,短軸長為
,短軸長為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若橢圓![]() 的左焦點為
的左焦點為![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,則在
兩點,則在![]() 軸上是否存在一個定點
軸上是否存在一個定點![]() 使得直線
使得直線![]() 的斜率互為相反數?若存在,求出定點
的斜率互為相反數?若存在,求出定點![]() 的坐標;若不存在,也請說明理由.
的坐標;若不存在,也請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究公司為了調查公眾對某事件的關注程度,在某年的連續6個月內,月份![]() 和關注人數
和關注人數![]() (單位:百)(
(單位:百)(![]() )數據做了初步處理,得到下面的散點圖及一些統計量的值.
)數據做了初步處理,得到下面的散點圖及一些統計量的值.

|
|
|
17.5 | 35 | 36.5 |
(1)由散點圖看出,可用線性回歸模型擬合y與x的關系,請用相關系數加以說明,并建立y關于x的回歸方程;
(2)經統計,調查材料費用v(單位:百元)與調查人數滿足函數關系![]() ,求材料費用的最小值,并預測此時的調查人數;
,求材料費用的最小值,并預測此時的調查人數;
(3)現從這6個月中,隨機抽取3個月份,求關注人數不低于1600人的月份個數![]() 分布列與數學期望.
分布列與數學期望.
參考公式:相關系數 ,若
,若![]() ,則y與x的線性相關程度相當高,可用線性回歸模型擬合y與x的關系.回歸方程
,則y與x的線性相關程度相當高,可用線性回歸模型擬合y與x的關系.回歸方程![]() 中斜率與截距的最小二乘估計公式分別為
中斜率與截距的最小二乘估計公式分別為 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,在
,在![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若![]() ,證明:
,證明: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)見解析
;(2)見解析
【解析】試題分析:(1)求出函數的導數,得到關于![]() 的方程組,解出即可;
的方程組,解出即可;
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,令
,令![]() , 利用導數研究其單調性可得
, 利用導數研究其單調性可得
![]() ,
,
從而證明![]() .
.
試題解析:((1)由題意![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,則
,則![]() ,與
,與![]() 矛盾,故
矛盾,故![]() ,
, ![]() .
.
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,
,
令![]() ,
,
![]() ,
,
令![]()
當![]() 時,
時, ![]() ,
, ![]() 單調遞減,且
單調遞減,且![]() ;
;
當![]() 時,
時, ![]() ,
, ![]() 單調遞增;且
單調遞增;且![]() ,
,
所以![]() 在
在![]() 上當單調遞減,在
上當單調遞減,在![]() 上單調遞增,且
上單調遞增,且![]() ,
,
故![]() ,
,
故![]() .
.
【點睛】本題考查利用函數的切線求參數的方法,以及利用導數證明不等式的方法,解題時要認真審題,注意導數性質的合理運用.
【題型】解答題
【結束】
22
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (
(![]() ,
, ![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相切;
相切;
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)在曲線![]() 上取兩點
上取兩點![]() ,
, ![]() 與原點
與原點![]() 構成
構成![]() ,且滿足
,且滿足![]() ,求面積
,求面積![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com