
【題目】已知函數f(x)= ![]() .
.
(Ⅰ)若a=﹣1,證明:函數f(x)是(0,+∞)上的減函數;
(Ⅱ)若曲線y=f(x)在點(1,f(1))處的切線與直線x﹣y=0平行,求a的值;
(Ⅲ)若x>0,證明: ![]() (其中e=2.71828…是自然對數的底數).
(其中e=2.71828…是自然對數的底數).
【答案】解:(Ⅰ)當a=﹣1時,f(x)= ![]() ,
,
∴函數的定義域為(﹣1,0)∪(0,+∞),
∴f′(x)= ![]() ,
,
設g(x)=x﹣(x+1)ln(x+1),
∴g′(x)=1﹣[ln(x+1)+1]=﹣ln(x+1),
∴g′(x)<0在(0,+∞)上恒成立,
∴g(x)在(0,+∞)上為減函數,
∴g(x)<g(0)=0,
∴f′(x)<0在(0,+∞)上恒成立,
∴f(x)在(0,+∞)上為減函數.
(Ⅱ)∵f′(x)= ![]() ,
,
∴k=f′(1)= ![]() ,
,
∵y=f(x)在點(1,f(1))處的切線與直線x﹣y=0平行
∴ ![]() =1,
=1,
即ln(1﹣a)= ![]() ,分別畫出y=ln(1﹣x)與y=
,分別畫出y=ln(1﹣x)與y= ![]() 的圖象,
的圖象,
又圖象可知交點為(0,0)
∴解得a=0.
(Ⅲ):∵ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
由(Ⅰ)知,當a=﹣1時,f(x)= ![]() 在(0,+∞)上為減函數,
在(0,+∞)上為減函數,
故要證原不等式成立,只需要證明:當x>0時,x<ex﹣1,
令h(x)=ex﹣1﹣x,
則h′(x)=ex﹣1>0,
∴h(x)在(0,+∞)上為增函數,
∴h(x)>h(0)=0,即x<ex﹣1,
∴f(x)>f(ex﹣1)
即 ![]() .
.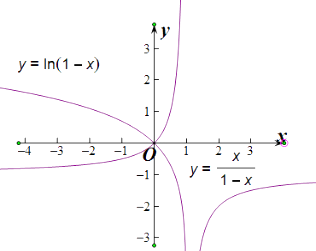
【解析】(Ⅰ) 先求導,得到f′(x)= ![]() ,再構造函數g(x)=x﹣(x+1)ln(x+1),求出g(x)的最大值為0,繼而得到f′(x)<0在(0,+∞)上恒成立,問題得以證明;(Ⅱ)欲求a的值,根據在點(1,f(1))處的切線方程,只須求出其斜率的值即可,故先利用導數求出在x=1處的導函數值,再結合導數的幾何意義即可求出切線的斜率,解方程即可得;(Ⅲ)
,再構造函數g(x)=x﹣(x+1)ln(x+1),求出g(x)的最大值為0,繼而得到f′(x)<0在(0,+∞)上恒成立,問題得以證明;(Ⅱ)欲求a的值,根據在點(1,f(1))處的切線方程,只須求出其斜率的值即可,故先利用導數求出在x=1處的導函數值,再結合導數的幾何意義即可求出切線的斜率,解方程即可得;(Ⅲ) ![]() =
= ![]() ,由(Ⅰ)的結論,故要證原不等式成立,只需要證明:當x>0時,x<ex﹣1,構造函數,利用導數和函數的最值的關系即可證明.
,由(Ⅰ)的結論,故要證原不等式成立,只需要證明:當x>0時,x<ex﹣1,構造函數,利用導數和函數的最值的關系即可證明.
【考點精析】關于本題考查的利用導數研究函數的單調性和函數的最大(小)值與導數,需要了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值才能得出正確答案.
比較,其中最大的是一個最大值,最小的是最小值才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】高考復習經過二輪“見多識廣”之后,為了研究考前“限時搶分”強化訓練次數![]() 與答題正確率
與答題正確率![]() ﹪的關系,對某校高三某班學生進行了關注統計,得到如下數據:
﹪的關系,對某校高三某班學生進行了關注統計,得到如下數據:
| 1 | 2 | 3 | 4 |
| 20 | 30 | 50 | 60 |
(1)求![]() 關于
關于![]() 的線性回歸方程,并預測答題正確率是100﹪的強化訓練次數;
的線性回歸方程,并預測答題正確率是100﹪的強化訓練次數;
(2)若用![]() 表示統計數據的“強化均值”(精確到整數),若“強化均值”的標準差在區間
表示統計數據的“強化均值”(精確到整數),若“強化均值”的標準差在區間![]() 內,則強化訓練有效,請問這個班的強化訓練是否有效?
內,則強化訓練有效,請問這個班的強化訓練是否有效?
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
 ,
,![]() =
=![]() -
-![]()
![]() ,
,
樣本數據![]() 的標準差為:
的標準差為: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的短軸長為2,離心率e=
=1(a>b>0)的短軸長為2,離心率e= ![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)若直線l:y=kx+m與橢圓交于不同的兩點A,B,與圓x2+y2= ![]() 相切于點M.
相切于點M.
(i)證明:OA⊥OB(O為坐標原點);
(ii)設λ= ![]() ,求實數λ的取值范圍.
,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)在R上存在導數f′(x),對任意的x∈R,有f(﹣x)+f(x)=x2 , 且x∈(0,+∞)時,f′(x)>x.若f(2﹣a)﹣f(a)≥2﹣2a,則實數a的取值范圍為( )
A.[1,+∞)
B.(﹣∞,1]
C.(﹣∞,2]
D.[2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() ,其中
,其中![]() 是不等于零的常數。
是不等于零的常數。
(1)寫出![]() 的定義域;
的定義域;
(2)求![]() 的單調遞增區間;
的單調遞增區間;
(3)已知函數![]() ,定義:
,定義:![]() ,
,![]() .其中,
.其中,![]() 表示函數
表示函數![]() 在
在![]() 上的最小值,
上的最小值,![]() 表示函數
表示函數![]() 在
在![]() 上的最大值.例如:
上的最大值.例如:![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,當
,當![]() 時,設
時,設![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() ,
,![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設0<a<1,已知函數f(x)= 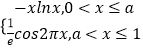 ,若對任意b∈(0,
,若對任意b∈(0, ![]() ),函數g(x)=f(x)﹣b至少有兩個零點,則a的取值范圍是( )
),函數g(x)=f(x)﹣b至少有兩個零點,則a的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖ABCD是平面四邊形,∠ADB=∠BCD=90°,AB=4,BD=2.
(Ⅰ)若BC=1,求AC的長;
(Ⅱ)若∠ACD=30°,求tan∠BDC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸與短軸之和為6,橢圓上任一點到兩焦點
的長軸與短軸之和為6,橢圓上任一點到兩焦點![]() ,
, ![]() 的距離之和為4.
的距離之和為4.
(1)求橢圓的標準方程;
(2)若直線![]() :
: ![]() 與橢圓交于
與橢圓交于![]() ,
, ![]() 兩點,
兩點, ![]() ,
, ![]() 在橢圓上,且
在橢圓上,且![]() ,
, ![]() 兩點關于直線
兩點關于直線![]() 對稱,問:是否存在實數
對稱,問:是否存在實數![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com