
【題目】已知拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,點(diǎn)
,點(diǎn)![]() 與
與![]() 關(guān)于坐標(biāo)原點(diǎn)對(duì)稱,直線
關(guān)于坐標(biāo)原點(diǎn)對(duì)稱,直線![]() 垂直于
垂直于![]() 軸,垂足為
軸,垂足為![]() ,與拋物線交于不同的兩點(diǎn)
,與拋物線交于不同的兩點(diǎn)![]() ,
, ![]() ,且
,且![]() .
.
(1)求點(diǎn)![]() 的橫坐標(biāo).
的橫坐標(biāo).
(2)若以![]() ,
, ![]() 為焦點(diǎn)的橢圓
為焦點(diǎn)的橢圓![]() 過(guò)點(diǎn)
過(guò)點(diǎn)
(ⅰ)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(ⅱ)過(guò)點(diǎn)![]() 作直線
作直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點(diǎn),設(shè)
兩點(diǎn),設(shè)![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .(2)(ⅰ)
.(2)(ⅰ)![]() (ⅱ)
(ⅱ)
【解析】試題分析:(1)由對(duì)稱性寫(xiě)出![]() 坐標(biāo),同時(shí)由對(duì)稱性可設(shè)
坐標(biāo),同時(shí)由對(duì)稱性可設(shè)![]() ,
, ![]() ,由數(shù)量積的坐標(biāo)運(yùn)算可解得T點(diǎn)坐標(biāo)。(2)由(1)得
,由數(shù)量積的坐標(biāo)運(yùn)算可解得T點(diǎn)坐標(biāo)。(2)由(1)得![]() ,待定系數(shù)及點(diǎn)
,待定系數(shù)及點(diǎn)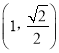 在橢圓上可求得橢圓方程。由
在橢圓上可求得橢圓方程。由![]() ,得
,得![]() ,且
,且![]() ,結(jié)合韋達(dá)可求得
,結(jié)合韋達(dá)可求得![]() ,把
,把![]() 通過(guò)坐標(biāo)表示寫(xiě)成關(guān)于k的函數(shù)關(guān)系,即可求得范圍。
通過(guò)坐標(biāo)表示寫(xiě)成關(guān)于k的函數(shù)關(guān)系,即可求得范圍。
試題解析:(1)由題意,得![]() ,
, ![]() ,
,
設(shè)![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
, ![]()
由![]()
得![]() ,即
,即![]() ,①
,①
又![]() 在拋物線上,則
在拋物線上,則![]() ,②
,②
聯(lián)立①②易得![]() ,則點(diǎn)
,則點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .
.
(2)(ⅰ)設(shè)橢圓的半焦距為![]() ,由題意,得
,由題意,得![]()
設(shè)橢圓![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() (
(![]() ),
),
則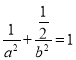 ,③
,③
![]() ,④
,④
將④代入③,解得![]() 或
或![]() (舍去)
(舍去)
所以![]()
故橢圓![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() .
.
(ⅱ)由題意分析知直線![]() 的斜率不為
的斜率不為![]() ,
,
設(shè)直線![]() 的方程為
的方程為![]()
將直線![]() 的方程代入
的方程代入![]() 中,得
中,得![]()
設(shè)![]() ,
, ![]() ,
, ![]() ,則由根與系數(shù)的關(guān)系,
,則由根與系數(shù)的關(guān)系,
可得![]() ,⑤
,⑤
![]() ⑥
⑥
因?yàn)?/span>![]() ,所以
,所以![]() ,且
,且![]() .
.
將⑤式平方除以⑥式,
得![]()
![]()
由![]()
![]()
![]()
![]() ,所以
,所以![]()
因?yàn)?/span>![]() ,
, ![]()
所以![]() .
.
又![]() ,所以
,所以![]()
故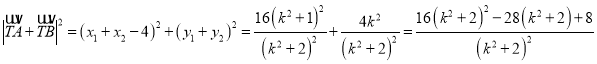
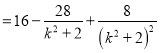
令![]() ,因?yàn)?/span>
,因?yàn)?/span>![]()
所以![]() ,即
,即![]() ,
,
所以![]()
而![]() ,所以
,所以
所以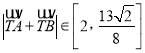


 口算題卡加應(yīng)用題集訓(xùn)系列答案
口算題卡加應(yīng)用題集訓(xùn)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知向量![]() ,
,![]() ,角
,角![]() ,
,![]() ,
,![]() 為
為![]() 的內(nèi)角,其所對(duì)的邊分別為
的內(nèi)角,其所對(duì)的邊分別為![]() ,
,![]() ,
,![]() .
.
(1)當(dāng)![]() 取得最大值時(shí),求角
取得最大值時(shí),求角![]() 的大小;
的大小;
(2)在(1)成立的條件下,當(dāng)![]() 時(shí),求
時(shí),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)拋物線的頂點(diǎn)在坐標(biāo)原點(diǎn),焦點(diǎn)![]() 在
在![]() 軸正半軸上,過(guò)點(diǎn)
軸正半軸上,過(guò)點(diǎn)![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點(diǎn),線段
兩點(diǎn),線段![]() 的長(zhǎng)是
的長(zhǎng)是![]() ,
, ![]() 的中點(diǎn)到
的中點(diǎn)到![]() 軸的距離是
軸的距離是![]() .
.
(1)求拋物線的標(biāo)準(zhǔn)方程;
(2)過(guò)點(diǎn)![]() 作斜率為
作斜率為![]() 的直線與拋物線交于
的直線與拋物線交于![]() 兩點(diǎn),直線
兩點(diǎn),直線![]() 交拋物線于
交拋物線于![]() ,
,
①求證: ![]() 軸為
軸為![]() 的角平分線;
的角平分線;
②若![]() 交拋物線于
交拋物線于![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
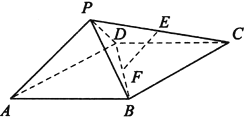
【題目】如圖,四棱錐P—ABCD中,ABCD為矩形,△PAD為等腰直角三角形,
∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分別為PC和BD的中點(diǎn).
(1)證明:EF∥面PAD;
(2)證明:面PDC⊥面PAD;
(3)求四棱錐P—ABCD的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,橢圓C: ![]() =1(a>b>0)過(guò)點(diǎn)P(1,
=1(a>b>0)過(guò)點(diǎn)P(1, ![]() ).離心率為
).離心率為![]() .
.
(1)求橢圓C的方程;
(2)設(shè)直線l與橢圓C交于A,B兩點(diǎn).
①若直線l過(guò)橢圓C的右焦點(diǎn),記△ABP三條邊所在直線的斜率的乘積為t.
求t的最大值;
②若直線l的斜率為![]() ,試探究OA2+ OB2是否為定值,若是定值,則求出此
,試探究OA2+ OB2是否為定值,若是定值,則求出此
定值;若不是定值,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】直角坐標(biāo)系![]() 和極坐標(biāo)系
和極坐標(biāo)系![]() 的原點(diǎn)與極點(diǎn)重合,
的原點(diǎn)與極點(diǎn)重合, ![]() 軸正半軸與極軸重合,單位長(zhǎng)度相同,在直角坐標(biāo)系下,曲線C的參數(shù)方程為
軸正半軸與極軸重合,單位長(zhǎng)度相同,在直角坐標(biāo)系下,曲線C的參數(shù)方程為![]() 為參數(shù))。
為參數(shù))。
(1)在極坐標(biāo)系下,曲線C與射線![]() 和射線
和射線![]() 分別交于A,B兩點(diǎn),求
分別交于A,B兩點(diǎn),求![]() 的面積;
的面積;
(2)在直角坐標(biāo)系下,直線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),求曲線C與直線
為參數(shù)),求曲線C與直線![]() 的交點(diǎn)坐標(biāo)。
的交點(diǎn)坐標(biāo)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商場(chǎng)經(jīng)銷一批進(jìn)價(jià)為每件30元的商品,在市場(chǎng)試銷中發(fā)現(xiàn),此商品的銷售單價(jià)x(元)與日銷售量y(件)之間有如下表所示的關(guān)系:
x | 30 | 40 | 45 | 50 |
y | 60 | 30 | 15 | 0 |
在所給的坐標(biāo)圖紙中,根據(jù)表中提供的數(shù)據(jù),描出實(shí)數(shù)對(duì)(x,y)的對(duì)應(yīng)點(diǎn),并確定y與x的一個(gè)函數(shù)關(guān)系式;

(2)設(shè)經(jīng)營(yíng)此商品的日銷售利潤(rùn)為P元,根據(jù)上述關(guān)系,寫(xiě)出P關(guān)于x的函數(shù)關(guān)系式,并指出銷售單價(jià)x為多少元時(shí),才能獲得最大日銷售利潤(rùn)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系中,以原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,點(diǎn)A的極坐標(biāo)為(3, ![]() ),點(diǎn)B的極坐標(biāo)為(6,
),點(diǎn)B的極坐標(biāo)為(6, ![]() ),曲線C:(x﹣1)2+y2=1
),曲線C:(x﹣1)2+y2=1
(1)求曲線C和直線AB的極坐標(biāo)方程;
(2)過(guò)點(diǎn)O的射線l交曲線C于M點(diǎn),交直線AB于N點(diǎn),若|OM||ON|=2,求射線l所在直線的直角坐標(biāo)方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了監(jiān)控某種零件的一條生產(chǎn)線的生產(chǎn)過(guò)程,檢驗(yàn)員每天從該生產(chǎn)線上隨機(jī)抽取16個(gè)零件,并測(cè)量其尺寸(單位: ![]() ).根據(jù)長(zhǎng)期生產(chǎn)經(jīng)驗(yàn),可以認(rèn)為這條生產(chǎn)線正常狀態(tài)下生產(chǎn)的零件的尺寸服從正態(tài)分布
).根據(jù)長(zhǎng)期生產(chǎn)經(jīng)驗(yàn),可以認(rèn)為這條生產(chǎn)線正常狀態(tài)下生產(chǎn)的零件的尺寸服從正態(tài)分布![]() .
.
(1)假設(shè)生產(chǎn)狀態(tài)正常,記![]() 表示一天內(nèi)抽取的16個(gè)零件中其尺寸在
表示一天內(nèi)抽取的16個(gè)零件中其尺寸在![]() 之外的零件數(shù),求
之外的零件數(shù),求![]() 及
及![]() 的數(shù)學(xué)期望;
的數(shù)學(xué)期望;
(2)一天內(nèi)抽檢零件中,如果出現(xiàn)了尺寸在![]() 之外的零件,就認(rèn)為這條生產(chǎn)線在這一天的生產(chǎn)過(guò)程可能出現(xiàn)了異常情況,需對(duì)當(dāng)天的生產(chǎn)過(guò)程進(jìn)行檢查.
之外的零件,就認(rèn)為這條生產(chǎn)線在這一天的生產(chǎn)過(guò)程可能出現(xiàn)了異常情況,需對(duì)當(dāng)天的生產(chǎn)過(guò)程進(jìn)行檢查.
(ⅰ)試說(shuō)明上述監(jiān)控生產(chǎn)過(guò)程方法的合理性;
(ⅱ)下面是檢驗(yàn)員在一天內(nèi)抽取的16個(gè)零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
經(jīng)計(jì)算得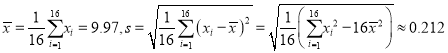 ,其中
,其中![]() 為
為
抽取的第![]() 個(gè)零件的尺寸,
個(gè)零件的尺寸, ![]() .
.
用樣本平均數(shù)![]() 作為
作為![]() 的估計(jì)值
的估計(jì)值![]() ,用樣本標(biāo)準(zhǔn)差
,用樣本標(biāo)準(zhǔn)差![]() 作為
作為![]() 的估計(jì)值
的估計(jì)值![]() ,利用估計(jì)值判斷是否需對(duì)當(dāng)天的生產(chǎn)過(guò)程進(jìn)行檢查?剔除
,利用估計(jì)值判斷是否需對(duì)當(dāng)天的生產(chǎn)過(guò)程進(jìn)行檢查?剔除![]() 之外的數(shù)據(jù),用剩下的數(shù)據(jù)估計(jì)
之外的數(shù)據(jù),用剩下的數(shù)據(jù)估計(jì)![]() 和
和![]() (精確到0.01).
(精確到0.01).
附:若隨機(jī)變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,則
,則![]() ,
, ![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com