
【題目】[2018·郴州期末]已知三棱錐![]() 中,
中,![]() 垂直平分
垂直平分![]() ,垂足為
,垂足為![]() ,
,![]() 是面積為
是面積為![]() 的等邊三角形,
的等邊三角形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,垂足為
,垂足為![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.
(1)證明:![]() 平面
平面![]() ;
;
(2)求![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
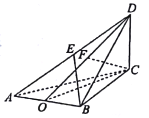
【答案】(1)見解析(2)![]()
【解析】試題分析:
(1)要證線面垂直,一般先證線線垂直,這可由![]() 和
和![]() 是等邊三角形及O是AB中點易得;
是等邊三角形及O是AB中點易得;
(2)要求直線與平面所成的角,一種方法作出線面角的平面角,然后解三角形得結論,也可建立空間直角坐標系,如解析中的坐標系,寫出各點坐標,求出直線的方向向量與平面的法向量,由方向向量與法向量的夾角與直線和平面所成角互余可得.
試題解析:
(1)證明:∵![]() 垂直平分
垂直平分![]() ,垂足為
,垂足為![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 是等邊三角形.
是等邊三角形.
又![]() 是等邊三角形.
是等邊三角形.
∴![]() 是
是![]() 中點,
中點,![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)解:由(1)知![]() ,平面
,平面![]() 平面
平面![]() .
.
因為平面![]() 與平面
與平面![]() 的交線為
的交線為![]() .
.
∵![]() 平面
平面![]() .∴
.∴![]() .
.
又等邊![]() 面積為
面積為![]() ,∴
,∴![]()
又![]() ,∴
,∴ ![]() 是
是![]() 中點.
中點.
如圖建立空間直角坐標系![]() ,
,
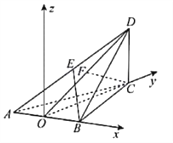
![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
,![]()
設平面![]() 的法向量為
的法向量為![]() ,則
,則
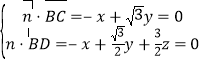 ,取
,取![]() ,則
,則![]() ,
,![]() .
.
即平面![]() 的一個法向量為
的一個法向量為![]() .
.
所以![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為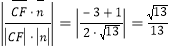 .
.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知拋物線
中,已知拋物線![]() 的焦點F在直線
的焦點F在直線![]() 上。
上。
(Ⅰ)求拋物線C的方程。
(Ⅱ)過點![]() 做互相垂直的兩條直線
做互相垂直的兩條直線![]() 與曲線C交于A,B兩點,
與曲線C交于A,B兩點,![]() 與曲線C交于E,F兩點,線段AB、EF的中點分別為M、N,求證:直線MN過定點P,并求出定點P的坐標。
與曲線C交于E,F兩點,線段AB、EF的中點分別為M、N,求證:直線MN過定點P,并求出定點P的坐標。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為打贏打好脫貧攻堅戰,實現建檔立卡貧困人員穩定增收,某地區把特色養殖確定為脫貧特色主導產業,助力鄉村振興.現計劃建造一個室內面積為![]() 平方米的矩形溫室大棚,并在溫室大棚內建兩個大小、形狀完全相同的矩形養殖池,其中沿溫室大棚前、后、左、右內墻各保留
平方米的矩形溫室大棚,并在溫室大棚內建兩個大小、形狀完全相同的矩形養殖池,其中沿溫室大棚前、后、左、右內墻各保留![]() 米寬的通道,兩養殖池之間保留2米寬的通道.設溫室的一邊長度為
米寬的通道,兩養殖池之間保留2米寬的通道.設溫室的一邊長度為![]() 米,如圖所示.
米,如圖所示.

(1)將兩個養殖池的總面積![]() 表示
表示![]() 為的函數,并寫出定義域;
為的函數,并寫出定義域;
(2)當溫室的邊長![]() 取何值時,總面積
取何值時,總面積![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四面體ABCD中,△ABC是等邊三角形,平面ABC⊥平面ABD,點M為棱AB的中點,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求證:AD⊥BC;
(Ⅱ)求異面直線BC與MD所成角的余弦值;
(Ⅲ)求直線CD與平面ABD所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(1)求![]() 的單調區間;
的單調區間;
(2)若![]() 圖像上任意一點
圖像上任意一點![]() 處的切線的斜率
處的切線的斜率![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若對于區間![]() 上任意兩個不相等的實數
上任意兩個不相等的實數![]() 都有
都有![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() ,
, ![]() ,若橢圓上一點
,若橢圓上一點![]() 滿足
滿足![]() ,且橢圓
,且橢圓![]() 過點
過點![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]()
![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作
作![]() 軸的垂線,交橢圓
軸的垂線,交橢圓![]() 于
于![]() ,求證:
,求證: ![]() ,
, ![]() ,
, ![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分別為
平面ABC,D,E,F,G分別為![]() ,AC,
,AC,![]() ,
,![]() 的中點,AB=BC=
的中點,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求證:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)證明:直線FG與平面BCD相交.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以“你我中國夢,全民建小康”為主題、“社會主義核心價值觀”為主線,為了了解![]() 兩個地區的觀眾對2018年韓國平昌冬奧會準備工作的滿意程度,對
兩個地區的觀眾對2018年韓國平昌冬奧會準備工作的滿意程度,對![]() 地區的100名觀眾進行統計,統計結果如下:
地區的100名觀眾進行統計,統計結果如下:
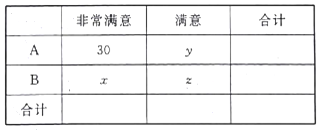
在被調查的全體觀眾中隨機抽取1名“非常滿意”的人是![]() 地區的概率為0.45,且
地區的概率為0.45,且![]() .
.
(Ⅰ)現從100名觀眾中用分層抽樣的方法抽取20名進行問卷調查,則應抽取“滿意”的![]() 地區的人數各是多少?
地區的人數各是多少?
(Ⅱ)在(Ⅰ)抽取的“滿意”的觀眾中,隨機選出3人進行座談,求至少有兩名是![]() 地區觀眾的概率?
地區觀眾的概率?
(Ⅲ)完成上述表格,并根據表格判斷是否有![]() 的把握認為觀眾的滿意程度與所在地區有關系?
的把握認為觀眾的滿意程度與所在地區有關系?
附: 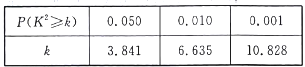 ,
, 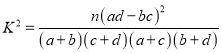 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列![]() 滿足:對于任意
滿足:對于任意![]() 均為數列
均為數列![]() 中的項,則稱數列
中的項,則稱數列![]() 為“
為“![]() 數列”.
數列”.
(1)若數列![]() 的前
的前![]() 項和
項和![]() ,求證:數列
,求證:數列![]() 為“
為“![]() 數列”;
數列”;
(2)若公差為![]() 的等差數列
的等差數列![]() 為“
為“![]() 數列”,求
數列”,求![]() 的取值范圍;
的取值范圍;
(3)若數列![]() 為“
為“![]() 數列”,
數列”,![]() ,且對于任意
,且對于任意![]() ,均有
,均有![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com