
【題目】若數(shù)列![]() 滿足:對于任意
滿足:對于任意![]() 均為數(shù)列
均為數(shù)列![]() 中的項,則稱數(shù)列
中的項,則稱數(shù)列![]() 為“
為“![]() 數(shù)列”.
數(shù)列”.
(1)若數(shù)列![]() 的前
的前![]() 項和
項和![]() ,求證:數(shù)列
,求證:數(shù)列![]() 為“
為“![]() 數(shù)列”;
數(shù)列”;
(2)若公差為![]() 的等差數(shù)列
的等差數(shù)列![]() 為“
為“![]() 數(shù)列”,求
數(shù)列”,求![]() 的取值范圍;
的取值范圍;
(3)若數(shù)列![]() 為“
為“![]() 數(shù)列”,
數(shù)列”,![]() ,且對于任意
,且對于任意![]() ,均有
,均有![]() ,求數(shù)列
,求數(shù)列![]() 的通項公式.
的通項公式.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)先利用項和公式計算出an=4n-2,再利用“![]() 數(shù)列”證明.(2)利用“
數(shù)列”證明.(2)利用“![]() 數(shù)列”的性質(zhì)求
數(shù)列”的性質(zhì)求![]() 的取值范圍.(3)先證明數(shù)列{an}為等差數(shù)列,再轉(zhuǎn)化an<a
的取值范圍.(3)先證明數(shù)列{an}為等差數(shù)列,再轉(zhuǎn)化an<a![]() -a<an+1,再轉(zhuǎn)化為n(2t2-t)>t2-3t+1,n(t-2t2)>2t-t2-1,分析得到公差t=
-a<an+1,再轉(zhuǎn)化為n(2t2-t)>t2-3t+1,n(t-2t2)>2t-t2-1,分析得到公差t=![]() ,求出數(shù)列
,求出數(shù)列![]() 的通項公式.
的通項公式.
詳解:(1)當n≥2時,an=Sn-Sn-1=2n2-2(n-1)2=4n-2,
又a1=S1=2=4×1-2,所以an=4n-2.
所以an+|an+1-an+2|=4n-2+4=4(n+1)-2為數(shù)列{an}的第n+1項,
因此數(shù)列{an}為“T 數(shù)列”.
(2)因為數(shù)列{an}是公差為d的等差數(shù)列,
所以an+|an+1-an+2|=a1+(n-1) d+|d|.
因為數(shù)列{an}為“T 數(shù)列”,
所以任意n∈N*,存在m∈N*,使得a1+(n-1) d+|d|=am,即有(m-n) d=|d|.
①若d≥0,則存在m=n+1∈N*,使得(m-n) d=|d|,
②若d<0,則m=n-1.
此時,當n=1時,m=0不為正整數(shù),所以d<0不符合題意. 綜上,d≥0.
(3)因為an<an+1,所以an+|an+1-an+2|=an+an+2-an+1.
又因為an<an+an+2-an+1=an+2-(an+1-an)<an+2,且數(shù)列{an}為“T數(shù)列”,
所以an+an+2-an+1=an+1,即an+an+2=2an+1,
所以數(shù)列{an}為等差數(shù)列.
設數(shù)列{an}的公差為t(t>0),則有an=1+(n-1)t,
由an<a![]() -a<an+1,得1+(n-1)t<t[2+(2n-1)t]<1+nt,
-a<an+1,得1+(n-1)t<t[2+(2n-1)t]<1+nt,
整理得n(2t2-t)>t2-3t+1, ①
n(t-2t2)>2t-t2-1. ②
若2t2-t<0,取正整數(shù)N0>![]() ,
,
則當n>N0時,n(2t2-t)<(2t2-t) N0<t2-3t+1,與①式對于任意n∈N*恒成立相矛盾,
因此2t2-t≥0.
同樣根據(jù)②式可得t-2t2≥0,
所以2t2-t=0.又t>0,所以t=![]() .
.
經(jīng)檢驗當t=![]() 時,①②兩式對于任意n∈N*恒成立,
時,①②兩式對于任意n∈N*恒成立,
所以數(shù)列{an}的通項公式為an=1+![]() (n-1)=
(n-1)=![]() .
.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數(shù)學 來源: 題型:
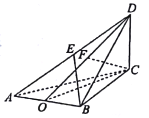
【題目】[2018·郴州期末]已知三棱錐![]() 中,
中,![]() 垂直平分
垂直平分![]() ,垂足為
,垂足為![]() ,
,![]() 是面積為
是面積為![]() 的等邊三角形,
的等邊三角形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,垂足為
,垂足為![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.
(1)證明:![]() 平面
平面![]() ;
;
(2)求![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知動點P到定點![]() 的距離比它到直線
的距離比它到直線![]() 的距離小2,設動點P的軌跡為曲線C.
的距離小2,設動點P的軌跡為曲線C.
![]() 求曲線C的方程;
求曲線C的方程;
![]() 若直線
若直線![]() 與曲線C和圓
與曲線C和圓![]() 從左至右的交點依次為A,B,C,D求
從左至右的交點依次為A,B,C,D求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題中正確的個數(shù)是( )
①命題“任意![]() ”的否定是“任意
”的否定是“任意![]() ;
;
②命題“若![]() ,則
,則![]() ”的逆否命題是真命題;
”的逆否命題是真命題;
③若命題![]() 為真,命題
為真,命題![]() 為真,則命題
為真,則命題![]() 且
且![]() 為真;
為真;
④命題“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”.
”.
A. ![]() 個 B.
個 B. ![]() 個 C.
個 C. ![]() 個 D.
個 D. ![]() 個
個
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】質(zhì)檢部門對某工廠甲、乙兩個車間生產(chǎn)的12個零件質(zhì)量進行檢測.甲、乙兩個車間的零件質(zhì)量(單位:克)分布的莖葉圖如圖所示.零件質(zhì)量不超過20克的為合格.
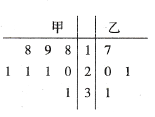
(1)從甲、乙兩車間分別隨機抽取2個零件,求甲車間至少一個零件合格且乙車間至少一個零件合格的概率;
(2)質(zhì)檢部門從甲車間8個零件中隨機抽取4件進行檢測,若至少2件合格,檢測即可通過,若至少3 件合格,檢測即為良好,求甲車間在這次檢測通過的條件下,獲得檢測良好的概率;
(3)若從甲、乙兩車間12個零件中隨機抽取2個零件,用![]() 表示乙車間的零件個數(shù),求
表示乙車間的零件個數(shù),求![]() 的分布列與數(shù)學期望.
的分布列與數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某食品的保鮮時間y(單位:小時)與儲存溫度x(單位:![]() )滿足函數(shù)關系
)滿足函數(shù)關系![]() (k,m為常數(shù)).若該食品在0
(k,m為常數(shù)).若該食品在0![]() 的保鮮時間是64小時,在18
的保鮮時間是64小時,在18![]() 的保鮮時間是16小時,則該食品在36
的保鮮時間是16小時,則該食品在36![]() 的保鮮時間是( )
的保鮮時間是( )
A.4小時B.8小時C.16小時D.32小時
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】探究函數(shù)![]() ,
,![]() 上的最小值,并確定取得最小值時
上的最小值,并確定取得最小值時![]() 的值,列表如下:
的值,列表如下:
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| … | 14 | 7 | 5.34 | 5.11 | 5.01 | 5 | 5.01 | 5.04 | 5.08 | 5.67 | 7 | 8.6 | 12.14 | … |
(1)觀察表中![]() 值隨
值隨![]() 值變化趨勢特點,請你直接寫出函數(shù)
值變化趨勢特點,請你直接寫出函數(shù)![]() ,
,![]() 的單調(diào)區(qū)間,并指出當
的單調(diào)區(qū)間,并指出當![]() 取何值時函數(shù)的最小值為多少;
取何值時函數(shù)的最小值為多少;
(2)用單調(diào)性定義證明函數(shù)![]() 在
在![]() 上的單調(diào)性.
上的單調(diào)性.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】[2018·江西聯(lián)考]交強險是車主必須為機動車購買的險種,若普通6座以下私家車投保交強險第一年的費用(基準保費)統(tǒng)一為![]() 元,在下一年續(xù)保時,實行的是費率浮動機制,保費與上一年度車輛發(fā)生道路交通事故的情況相聯(lián)系,發(fā)生交通事故的次數(shù)越多,費率也就越高,具體浮動情況如表:
元,在下一年續(xù)保時,實行的是費率浮動機制,保費與上一年度車輛發(fā)生道路交通事故的情況相聯(lián)系,發(fā)生交通事故的次數(shù)越多,費率也就越高,具體浮動情況如表:
交強險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
| 上一個年度未發(fā)生有責任道路交通事故 | 下浮10% |
| 上兩個年度未發(fā)生有責任道路交通事故 | 下浮20% |
| 上三個及以上年度未發(fā)生有責任道路交通事故 | 下浮30% |
| 上一個年度發(fā)生一次有責任不涉及死亡的道路交通事故 | 0% |
| 上一個年度發(fā)生兩次及兩次以上有責任道路交通事故 | 上浮10% |
| 上一個年度發(fā)生有責任道路交通死亡事故 | 上浮30% |
某機構(gòu)為了研究某一品牌普通6座以下私家車的投保情況,隨機抽取了80輛車齡已滿三年的該品牌同型號私家車的下一年續(xù)保時的情況,統(tǒng)計得到了下面的表格:
類型 |
|
|
|
|
| |
數(shù)量 | 20 | 10 | 10 | 20 | 15 | 5 |
以這80輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(1)按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規(guī)定,![]() .某同學家里有一輛該品牌車且車齡剛滿三年,記X為該品牌車在第四年續(xù)保時的費用,求X的分布列與數(shù)學期望值;(數(shù)學期望值保留到個位數(shù)字)
.某同學家里有一輛該品牌車且車齡剛滿三年,記X為該品牌車在第四年續(xù)保時的費用,求X的分布列與數(shù)學期望值;(數(shù)學期望值保留到個位數(shù)字)
(2)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強險保費高于基本保費的車輛記為事故車.假設購進一輛事故車虧損4000元,一輛非事故車盈利8000元:
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車,求這三輛車中至多有一輛事故車的概率;
②若該銷售商一次購進100輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com