【題目】試求出最小的正整數
，使得同時滿足：
（1）
（
對表示不大于
的最大整數）；
（2）
被190除所得的余數為11.
【答案】
【解析】
由條件（1）可知
.
否則，若
，則有
，這與條件（1）矛盾.故必有.
令
（
為正整數）代入條件（1）中的不等式得
，
即
. ①
由于
為嚴格遞增函數，而
滿足式①，
不滿足式①，
所以，式①的解為
.從而條件（1）中不等式的解為
.
又因99與190互質，所以，由歐拉定理得
，
即
. ②
引理：若
，
是正整數，而
是最小的正整數，使得
，則必有
.
引理的證明：顯然
（由的最小性）.
記
（
，
，且
）.
由及，得
，
即
.
再由為正整數且為最小者及，知只有
.于是，有
，即.
回到原題.
由式②及引理知
.所以，
.
下面求的值.
注意到
，
，
，
，
，
，
，
，
所以，
.
現有
，而
，且99與190互質，所以有
.
由及上述引理，得
，即
.
再由，得
.于是，
，
.
故所求的最小正整數.
科目：高中數學 來源： 題型：
【題目】我市南澳縣是廣東唯一的海島縣，海區面積廣闊，發展太平洋牡蠣養殖業具有得天獨厚的優勢，所產的“南澳牡蠣”是中國國家地理標志產品，產量高、肉質肥、營養好，素有“海洋牛奶精品”的美譽．根據養殖規模與以往的養殖經驗，產自某南澳牡蠣養殖基地的單個“南澳牡蠣”質量（克）在正常環境下服從正態分布
．
（1）購買10只該基地的“南澳牡蠣”，會買到質量小于20g的牡蠣的可能性有多大？
（2）2019年該基地考慮增加人工投入，現有以往的人工投入增量x（人）與年收益增量y（萬元）的數據如下：
人工投入增量x（人） | 2 | 3 | 4 | 6 | 8 | 10 | 13 |
年收益增量y（萬元） | 13 | 22 | 31 | 42 | 50 | 56 | 58 |
該基地為了預測人工投入增量為16人時的年收益增量，建立了y與x的兩個回歸模型：
模型①：由最小二乘公式可求得y與x的線性回歸方程：
；
模型②：由散點圖的樣本點分布，可以認為樣本點集中在曲線：
的附近，對人工投入增量x做變換，令
，則
，且有
．
（i）根據所給的統計量，求模型②中y關于x的回歸方程（精確到0.1）；
（ii）根據下列表格中的數據，比較兩種模型的相關指數
，并選擇擬合精度更高、更可靠的模型，預測人工投入增量為16人時的年收益增量．
回歸模型 | 模型① | 模型② |
回歸方程 |
|
|
| 182.4 | 79.2 |
附：若隨機變量
，則
，
；
樣本
的最小二乘估計公式為：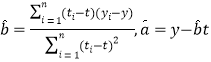
，
另，刻畫回歸效果的相關指數
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
、
、
為大于3的整數，將
的立方體分割為
個單位正方體，從一角的單位正方體起第
層、第
行、第
列的單位正方體記為
．求所有有序六元數組
的個數，使得一只螞蟻從
出發，經過每個小正方體恰一次到達
.（注）螞蟻可以從一個單位正方體爬到另一個與之有公共面的相鄰正方體．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
： 
的左、右焦點分別為
， 
為坐標原點， 
是雙曲線上在第一象限內的點，直線
分別交雙曲線
左、右支于另一點
， 
，且
，則雙曲線
的離心率為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】農歷戊戌年即將結束，為了迎接新年，小康、小梁、小譚、小劉、小林每人寫了一張心愿卡，設計了一個與此心愿卡對應的漂流瓶.現每人隨機的選擇一個漂流瓶將心愿卡放入，則事件“至少有兩張心愿卡放入對應的漂流瓶”的概率為___
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面上有12個點且任意三點不共線.以其中任意一點為始點、另一點為終點作向量且作出所有的向量，其中，三邊向量的和為零向量的三角形稱為“零三角形”.求以這12個點為頂點的零三角形個數的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
