
【題目】已知![]() 、
、![]() 、
、![]() 為大于3的整數,將
為大于3的整數,將![]() 的立方體分割為
的立方體分割為![]() 個單位正方體,從一角的單位正方體起第
個單位正方體,從一角的單位正方體起第![]() 層、第
層、第![]() 行、第
行、第![]() 列的單位正方體記為
列的單位正方體記為![]() .求所有有序六元數組
.求所有有序六元數組![]() 的個數,使得一只螞蟻從
的個數,使得一只螞蟻從![]() 出發,經過每個小正方體恰一次到達
出發,經過每個小正方體恰一次到達![]() .(注)螞蟻可以從一個單位正方體爬到另一個與之有公共面的相鄰正方體.
.(注)螞蟻可以從一個單位正方體爬到另一個與之有公共面的相鄰正方體.
【答案】見解析
【解析】
按照國際象棋棋盤的染色規則交替地將各個單位正方體染為黑色或白色,其中,![]() 為黑色.
為黑色.
當![]() 為偶數時,任兩個異色的小正方體滿足條件;當
為偶數時,任兩個異色的小正方體滿足條件;當![]() 為奇數時,任兩個黑色的小正方體滿足條件.
為奇數時,任兩個黑色的小正方體滿足條件.
首先證明三個引理.
引理l (i)在![]() 立方體中,異色的兩個小正方體滿足條件;
立方體中,異色的兩個小正方體滿足條件;
(ii)在![]() 立方體中,黑色的兩個小正方體滿足條件.
立方體中,黑色的兩個小正方體滿足條件.
引理l的證明 由文[1]加試第四題可證.
引理2 在![]() 立方體中,
立方體中,![]()
滿足條件,其中,![]() ,即
,即![]() 、
、![]() 異色.
異色.
引理2的證明 在第l層中,由引理l(i),有![]() 滿足條件,其路徑為
滿足條件,其路徑為![]()
![]() …
…![]() ,
,
其為黑白相間的.則在![]() 立方體中,對
立方體中,對![]() ,
,![]() ,用
,用
![]()
![]() …
…![]()
![]()
![]() …
…![]()
代替![]()
![]() ,而
,而![]()
![]() 不變.
不變.
【注】為同一層相鄰,為不同層相鄰.
故在![]() 立方體中,
立方體中,![]() 滿足條件.
滿足條件.
引理3 在![]() 立方體中,
立方體中,![]()
滿足條件,其中,![]() ,即
,即![]() 、
、![]() 異色.
異色.
引理3的證明 在第l層中,由引理l(i),有![]() (與
(與![]() 異色)滿足條件,取第2層中與
異色)滿足條件,取第2層中與![]() 相鄰的小正方體為
相鄰的小正方體為![]() ;類似有
;類似有![]()
![]() …
…![]() ,
,
其中,![]() 、
、![]() 分別為第
分別為第![]() 層與
層與![]() 、
、![]() 同色的小正方體
同色的小正方體
故在![]() 正方體中,
正方體中,![]() 滿足條件.
滿足條件.
回到原題.
(1)![]() 為偶數.
為偶數.
不妨設![]() 為偶數,異色的小正方體
為偶數,異色的小正方體![]() 、
、![]() 分別在第
分別在第![]() 、
、![]() 層(
層(![]() ).
).
若![]() ,則將
,則將![]() 立方體按
立方體按![]() 層、
層、![]() 層、
層、![]() 層分成三部分,在上、下兩部分應用引理2,在中間部分應用引理l(i)或引理3,得到在
層分成三部分,在上、下兩部分應用引理2,在中間部分應用引理l(i)或引理3,得到在![]() 立方體中的路徑
立方體中的路徑
![]()
![]()
![]() (
(![]() 、
、![]() 同引理3).
同引理3).
若![]() ,則將
,則將![]() 立方體按
立方體按![]() 層、
層、![]() 層分成兩部分,類似得在
層分成兩部分,類似得在![]() 立方體中的路徑
立方體中的路徑
![]()
![]() .
.
若![]() ,則將
,則將![]() 立方體按
立方體按![]() 層、
層、![]() 層、
層、![]() 層分成三部分.
層分成三部分.
在第![]() 層,由引理l(i)有
層,由引理l(i)有![]()
![]() …
…![]() .
.
取![]() ,則由引理2知在上、下兩部分中分別有
,則由引理2知在上、下兩部分中分別有![]() ,
,![]() 滿足條件.
滿足條件.
從而,在![]() 立方體中有路徑
立方體中有路徑
![]() …
…![]()
![]()
![]() …
…![]()
![]()
![]() …
…![]() ,其中,
,其中,![]() 、
、![]() 分別為第
分別為第![]() 層的小正方體
層的小正方體
(2)![]() 為奇數.
為奇數.
若黑色的小正方體![]() 、
、![]() 在
在![]() 立方體的對角,則由引理l(ii),仿引理2可構造
立方體的對角,則由引理l(ii),仿引理2可構造![]() 路徑滿足條件;否則,
路徑滿足條件;否則,![]() 方體有一面不含
方體有一面不含![]() 、
、![]() ,且
,且![]() 、
、![]() 到該面的投影不同.不妨設
到該面的投影不同.不妨設![]() 、
、![]() ,其中,
,其中,![]() 、
、![]() ,
,![]() .
.
將![]() 立方體先按第l層、第
立方體先按第l層、第![]() 層分成兩部分,再將后者按第
層分成兩部分,再將后者按第![]() 行、第
行、第![]() 行分成兩部分.
行分成兩部分.
因![]() 為偶數,所以,由(1)知在后兩部分內分別有
為偶數,所以,由(1)知在后兩部分內分別有![]() ,
,![]() 滿足條件,其中,
滿足條件,其中,![]() 、
、![]() 為第2層中的白色小正方體.
為第2層中的白色小正方體.
在第l層中分別取與![]() 、
、![]() 相鄰的黑色小正方體,記為
相鄰的黑色小正方體,記為![]() 、
、![]() .由引理1(ii)知
.由引理1(ii)知![]() 滿足條件.
滿足條件.
則![]() 立方體中有路徑
立方體中有路徑![]()
![]()
![]() .
.
故當![]() 為奇數時,所求為
為奇數時,所求為![]() ; ’
; ’
當![]() 為偶數時,所求為
為偶數時,所求為![]() .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的左焦點為
的左焦點為![]() ,且點
,且點![]() 在C上.
在C上.
![]() 求C的方程;
求C的方程;
![]() 設點P關于x軸的對稱點為點
設點P關于x軸的對稱點為點![]() 不經過P點且斜率為k的直線l與C交于A,B兩點,直線PA,PB分別與x軸交于點M,N,若
不經過P點且斜率為k的直線l與C交于A,B兩點,直線PA,PB分別與x軸交于點M,N,若![]() ,求k.
,求k.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線![]() ,直線l的參數方程為:
,直線l的參數方程為:![]() (
(![]() 為參數),直線l與曲線C分別交于M,N兩點.
為參數),直線l與曲線C分別交于M,N兩點.
(1)寫出曲線C的直角坐標方程和直線l的普通方程;
(2)若點![]() ,求
,求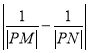 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為![]() (
(![]() 為參數,
為參數,![]() ,以
,以![]() 為極點,
為極點,![]() 軸非負半軸為極軸,建立極坐標系,曲線
軸非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程
的極坐標方程![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面上有7個點,每三點的兩兩連線都組成一個不等邊三角形.求證:一定可以找到4對三角形,使每對三角形的公共邊既是其中一個三角形的最長邊又是另一個三角形的最短邊.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定義域;
(2)判斷f(x)的奇偶性并予以證明;
(3)當a>1時,求使f(x)>0的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com