【題目】平面上有12個點(diǎn)且任意三點(diǎn)不共線.以其中任意一點(diǎn)為始點(diǎn)、另一點(diǎn)為終點(diǎn)作向量且作出所有的向量，其中，三邊向量的和為零向量的三角形稱為“零三角形”.求以這12個點(diǎn)為頂點(diǎn)的零三角形個數(shù)的最大值.
【答案】70
【解析】
設(shè)這12個點(diǎn)分別為
.這12個點(diǎn)確定的三角形共有
個，設(shè)以
為始點(diǎn)的向量數(shù)為
.
若以某三點(diǎn)為頂點(diǎn)的三角形為非零三角形，則有且僅有一個點(diǎn)是此三角形兩邊向量的始點(diǎn)，所以，以
為頂點(diǎn)之一且為兩邊始點(diǎn)的非零三角形有
個.從而，以這些點(diǎn)為頂點(diǎn)的三角形中非零三角形的總數(shù)為
.
因此，零三角形的個數(shù)為
.
先求的最小值.
因?yàn)?/span>
，所以，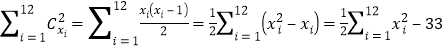
.
而非負(fù)整數(shù)
不超過11，故
有最小值.
由調(diào)整法知，當(dāng)
，即當(dāng)
時，取最小值366.
故的最小值為
.
因此，以這12個點(diǎn)為頂點(diǎn)的零三角形個數(shù)的最大值為70.
奪冠訓(xùn)練單元期末沖刺100分系列答案
新思維小冠軍100分作業(yè)本系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】選修4-4：坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系
中，曲線
： 
（
為參數(shù)， 
），在以坐標(biāo)原點(diǎn)為極點(diǎn)， 
軸的非負(fù)半軸為極軸的極坐標(biāo)系中，曲線
： 
.
（1）試將曲線
與
化為直角坐標(biāo)系
中的普通方程，并指出兩曲線有公共點(diǎn)時
的取值范圍；
（2）當(dāng)
時，兩曲線相交于
， 
兩點(diǎn)，求
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】試求出最小的正整數(shù)
，使得同時滿足：
（1）
（
對表示不大于
的最大整數(shù)）；
（2）
被190除所得的余數(shù)為11.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】將平面上每個點(diǎn)染為
種顏色之一，同時滿足：
（1）每種顏色的點(diǎn)都有無窮多個，且不全在同一條直線上；
（2）至少有一條直線上所有的點(diǎn)恰為兩種顏色．
求的最小值，使得存在互不同色的四個點(diǎn)共圓．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】從1，2，…，2011中最少應(yīng)選出多少個不同的數(shù)，才能保證選出的數(shù)中必存在三個不同的數(shù)構(gòu)成一個三角形的三邊長.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
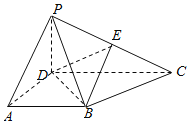
【題目】如圖，在四棱錐
中，
平面ABCD，底面ABCD為梯形，
，
，
，
，E為PC的中點(diǎn)．
證明：
平面PAD；
求二面角
的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
在
與
時都取得極值．
（1）求
的值與函數(shù)
的單調(diào)區(qū)間；
（2）若對
,不等式
恒成立，求
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
是定義在R上的函數(shù)
的導(dǎo)函數(shù)，且
，則
的大小關(guān)系為( )
A. a<b<c B. b<a<c C. c<a<b D. c<b<a
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com