【題目】已知f（x）= 
，g（x）= 
．
（1）當1≤x＜2時，求g（x）；
（2）當x∈R時，求g（x）的解析式，并畫出其圖象； 
（3）求方程xf[g（x）]=2g[f（x）]的解．
科目：高中數學 來源： 題型：
【題目】霧霾天氣對城市環境造成很大影響，按照國家環保部發布的標準：居民區的PM2.5（大氣中直徑小于或等于2.5微米的顆粒物）年平均濃度不得超過35微克/立方米.某市環保部門加強了對空氣質量的監測，抽取某居民區監測點的20天PM2.5的24小時平均濃度的監測數據，制成莖葉圖，如圖：
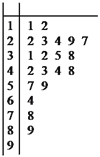
（Ⅰ）完成如下頻率分布表，并在所給的坐標系中畫出
的頻率分布直方圖；
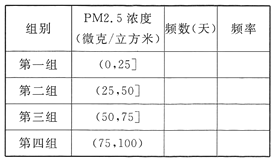
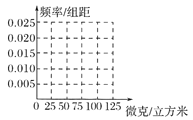
（Ⅱ）從樣本中PM2.5的24小時平均濃度超過50微克/立方米的天數中，隨機抽取2天，求恰好有一天PM2.5的24小時平均濃度超過75微克/立方米的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C的方程為： 
=1（a＞0），其焦點在x軸上，離心率e= 
．
（1）求該橢圓的標準方程；
（2）設動點P（x0 ， y0）滿足 
，其中O為坐標原點，M，N是橢圓C上的點，直線OM與ON的斜率之積為﹣ 
，求證：x02+2y02為定值．
（3）在（2）的條件下，問：是否存在兩個定點A，B，使得|PA|+|PB|為定值？若存在，給出證明；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是我國2008年至2014年生活垃圾無害化處理量（單位：億噸）的折線圖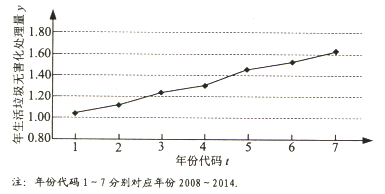 
（Ⅰ）由折線圖看出，可用線性回歸模型擬合y與t的關系，請用相關系數加以說明；
（Ⅱ）建立y關于t的回歸方程（系數精確到0.01），預測2017年我國生活垃圾無害化處理量．
參考數據： 
=9.32， 
yi=40.17， 
=0.55， 
≈2.646．
參考公式：相關系數r=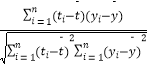 
回歸方程 
= 
+ 
t 中斜率和截距的最小二乘估計公式分別為： = 
， = ﹣ 
．
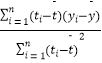查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC—A1B1C1中，AB=BC=BB1， 
，D為AC上的點，B1C∥平面A1BD；
（1）求證：BD⊥平面
；
（2）若
且
，求三棱錐A-BCB1的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設△ABC的內角A、B、C所對邊分別是a、b、c，已知B=60°，
（1）若b= 
，A=45°，求a；
（2）若a、b、c成等比數列，請判斷△ABC的形狀．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）是定義在R上的偶函數，且當x≤0時，f（x）=x2+2x．
（1）現已畫出函數f（x）在y軸左側的圖象，如圖所示，請補出完整函數f（x）的圖象，并根據圖象寫出函數f（x）的增區間； 
（2）寫出函數f（x）的解析式和值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中， 
平面
， 
，且， 
， 
， 
為線段
上一點， 
，且
為
的中點.
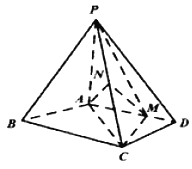
（Ⅰ）證明： 
平面
；
（Ⅱ）求證：平面
平面
；
（Ⅲ）求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）=ax2﹣2ax+b+1（a＞0）在區間[2，3]上有最大值4，最小值1．
（Ⅰ）求函數f（x）的解析式；
（Ⅱ）設g（x）= 
．若不等式g（2x）﹣k2x≥0對任意x∈[1，2]恒成立，求k的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
