
【題目】已知函數![]()
(1)函數![]() ,若
,若![]() 是
是![]() 的極值點,求
的極值點,求![]() 的值并討論
的值并討論![]() 的單調性;
的單調性;
(2)函數![]() 有兩個不同的極值點,其極小值為為
有兩個不同的極值點,其極小值為為![]() ,試比較
,試比較![]() 與
與![]() 的大小關系,并說明理由.
的大小關系,并說明理由.
【答案】(1)![]() ,在
,在![]() 單調遞減,在
單調遞減,在![]() 單調遞增(2)
單調遞增(2)![]()
【解析】試題分析:(1)求出函數![]() 的導數,根據
的導數,根據![]() 解出
解出![]() 的值,從而確定
的值,從而確定![]() 的表達式,進而求出單調區間;(2)對
的表達式,進而求出單調區間;(2)對![]() 求導,
求導, ![]() 有兩個不同的極值點,即方程
有兩個不同的極值點,即方程![]() 在
在![]() 有兩個不同的實根,運用判別式和韋達定理,可得到
有兩個不同的實根,運用判別式和韋達定理,可得到![]() ,列表求出
,列表求出![]() 的單調區間和最值,即可得出
的單調區間和最值,即可得出![]() ,再通過構造
,再通過構造![]() ,運用導數可知函數
,運用導數可知函數![]() 在
在![]() 單調遞減,從而得出
單調遞減,從而得出![]() .
.
試題解析:(1)![]()
![]() ,
,
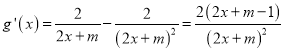 ,
,
因為![]() 是
是![]() 的極值點,所以
的極值點,所以![]() ,得
,得![]() ,
, ![]() ,
,
此時![]()
![]() ,
, 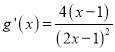 ,
,
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
所以![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
(2)![]()
![]() ,
,
![]()
![]() ,
,
因為![]() 有兩個不同的極值點,所以
有兩個不同的極值點,所以![]() 在
在![]() 有兩個不同的實根,設此兩根為
有兩個不同的實根,設此兩根為![]() ,
, ![]() ,且
,且![]() .
.
則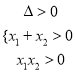 ,即
,即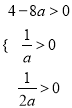 ,解得
,解得![]() .
.
![]() 與
與![]() 隨
隨![]() 的變化情況如下表:
的變化情況如下表:
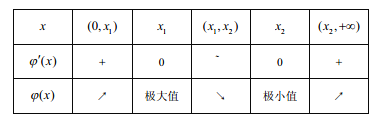
由表可知![]()
![]() ,
,
因為![]() ,所以
,所以![]() 代入上式得:
代入上式得:
![]() ,所以
,所以![]() ,
,
因為![]() ,且
,且![]() ,所以
,所以![]() .
.
令![]() ,則
,則![]() ,
,
當![]() 時,
時, ![]() ,即
,即![]() 在
在![]() 單調遞減,
單調遞減,
所以當![]() 時,有
時,有![]() ,
,
即![]() .
.
點睛:本題考查導數的綜合應用求單調性和極值,考查函數的單調性及運用,極值點的個數與方程根的關系,屬于中檔題.極值點的個數問題經常與導函數在定義域內的方程根個數相互轉化,一元二次方程在![]() 有兩個不同的實根,等價轉化為判別式大于
有兩個不同的實根,等價轉化為判別式大于![]() ,韋達定理寫出兩根和與積,分別大于
,韋達定理寫出兩根和與積,分別大于![]() 即可.
即可.


科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在
在 ![]() 上是減函數,求實數
上是減函數,求實數![]() 的取值范圍;
的取值范圍;
(3)令![]() ,是否存在實數
,是否存在實數![]() ,當
,當![]() (
(![]() 是自然對數的底數)時,函數
是自然對數的底數)時,函數![]() 的最小值是
的最小值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學高二年級開設五門大學先修課程,其中屬于數學學科的有兩門,分別是線性代數和微積分,其余三門分別為大學物理,商務英語以及文學寫作,年級要求每名學生只能選修其中一科,該校高二年級600名學生各科選課人數統計如下表:

其中選修數學學科的人數所占頻率為0.6,為了了解學生成績與選課情況之間的關系,用分層抽樣的方法從這600名學生中抽取10人進行分析.
(1)求![]() 和
和![]() 的取值以及抽取的10人中選修商務英語的學生人數;
的取值以及抽取的10人中選修商務英語的學生人數;
(2)選出的10名學生中恰好包含甲乙兩名同學,其中甲同學選修的是線性代數,乙同學選修的是大學物理,現從線性代數和大學物理兩個學科中隨機抽取3人,求這3人中正好有甲乙兩名同學的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在棱長均相等的正四棱錐![]() 中,
中, ![]() 為底面正方形的重心,
為底面正方形的重心, ![]() 分別為側棱
分別為側棱![]() 的中點,有下列結論:
的中點,有下列結論:
①![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③
;③![]() ;
;
④直線![]() 與直線
與直線![]() 所成角的大小為
所成角的大小為![]() .
.
其中正確結論的序號是__________.(寫出所有正確結論的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-5:不等式選講
已知函數f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若關于x的不等式f(x)≤|3m+1|有解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線C的極坐標方程為ρ﹣4cosθ+3ρsin2θ=0,以極點為原點,極軸為x軸的正半軸建立平面直角坐標系,直線l過點M(1,0),傾斜角為![]() .
.
(Ⅰ)求曲線C的直角坐標方程與直線l的參數方程;
(Ⅱ)若曲線C經過伸縮變換![]() 后得到曲線C′,且直線l與曲線C′交于A,B兩點,求|MA|+|MB|.
后得到曲線C′,且直線l與曲線C′交于A,B兩點,求|MA|+|MB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中點.
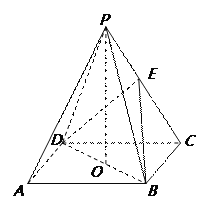
.求證:(Ⅰ)PA∥平面BDE;(Ⅱ)平面PAC⊥平面BDE;(III)若PB與底面所成的角為600, AB=2a,求三棱錐E-BCD的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com