
【題目】如圖1,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,過A,B分別作CD的垂線,垂足分別為E,F,已知
,過A,B分別作CD的垂線,垂足分別為E,F,已知![]() ,
,![]() ,將梯形ABCD沿AE,BF同側折起,使得平面
,將梯形ABCD沿AE,BF同側折起,使得平面![]() 平面ABFE,平面
平面ABFE,平面![]() 平面BCF,得到圖2.
平面BCF,得到圖2.
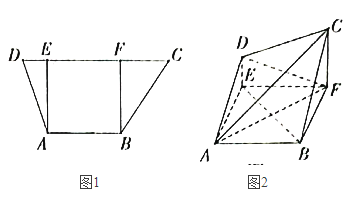
(1)證明:![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析.(2)![]()
【解析】
(1)設![]() ,取AC中點M,連接OM,DM,可證明四邊形DEOM為平行四邊形 可得
,取AC中點M,連接OM,DM,可證明四邊形DEOM為平行四邊形 可得![]() ,即得證;
,即得證;
(2)建立如圖空間直角坐標系,求解平面ADF,平面ADC的法向量,由二面角的向量公式即得解.
(1)設![]() ,取AC中點M,連接OM,DM
,取AC中點M,連接OM,DM
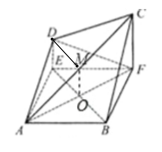
四邊形ABFE為正方形 ∴為AF中點 ∵M為AC中點 ∴![]()
∵平面![]() 平面ABFE
平面ABFE
平面![]() 平面
平面![]()
![]()
![]() 平面ABFE
平面ABFE
![]() 平面ADE
平面ADE
又∵平面![]() 平面BCF
平面BCF
∴平面![]() 平面ABFE 同理,
平面ABFE 同理,![]() 平面ABFE
平面ABFE
又∵![]() ,
,![]() ∴
∴![]()
∴![]()
∴四邊形DEOM為平行四邊形 ∴![]()
∵![]() 平面ADC,
平面ADC,![]() 平面ADC
平面ADC
∴平面ADC
(2)由題意EA,EF,ED兩兩垂直,以EA為x軸,EF為y軸,ED為z軸建立空間直角坐標系![]()
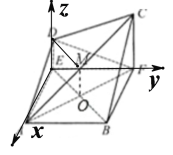
∴![]() ,
,![]() ,
,![]() ,
,![]()
設平面ADF的法向量為![]()
∵![]() ,
,![]()
∴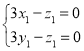
∴![]()
設平面ADC的法向量為![]()
∵![]()
∴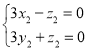
∴![]()
設二面角![]() 的平面角為θ,由圖像得θ為銳角,
的平面角為θ,由圖像得θ為銳角,
∴![]()


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】2016里約奧運會期間,小趙常看的4個電視頻道中有2個頻道在轉播奧運比賽,若小趙這時打開電視,隨機打開其中兩個頻道試看,那么,小趙所看到的第一個電視臺恰好沒有轉播奧運比賽,而第二個電視臺恰好在轉播奧運比賽的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲線y=f(x)上總存在兩點M(x1,y1),N(x2,y2),使曲線y=f(x)在M,N兩點處的切線互相平行,則x1+x2的取值范圍為
,k∈[4,+∞),曲線y=f(x)上總存在兩點M(x1,y1),N(x2,y2),使曲線y=f(x)在M,N兩點處的切線互相平行,則x1+x2的取值范圍為
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】唐代詩人李欣的是![]() 古從軍行
古從軍行![]() 開頭兩句說“百日登山望烽火,黃昏飲馬傍交河”詩中隱含著一個有缺的數學故事“將軍飲馬”的問題,即將軍在觀望烽火之后從山腳下某處出發,先到河邊飲馬后再回到軍營,怎樣走才能使總路程最短?在平面直角坐標系中,設軍營所在區域為
開頭兩句說“百日登山望烽火,黃昏飲馬傍交河”詩中隱含著一個有缺的數學故事“將軍飲馬”的問題,即將軍在觀望烽火之后從山腳下某處出發,先到河邊飲馬后再回到軍營,怎樣走才能使總路程最短?在平面直角坐標系中,設軍營所在區域為![]() ,若將軍從
,若將軍從![]() 出發,河岸線所在直線方程
出發,河岸線所在直線方程![]() ,并假定將軍只要到達軍營所在區域即回到軍營,則“將軍飲馬”的最短總路程為( )
,并假定將軍只要到達軍營所在區域即回到軍營,則“將軍飲馬”的最短總路程為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以該直角坐標系的原點
為參數),以該直角坐標系的原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,交曲線
兩點,交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數![]() 在某一個周期內的圖象時,列表并填入了部分數據,如下表:
在某一個周期內的圖象時,列表并填入了部分數據,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
(1)請將上表數據補充完整,填寫在答題卡上相應位置,并直接寫出函數![]() 的解析式;
的解析式;
(2)將![]() 圖象上所有點向左平行移動
圖象上所有點向左平行移動![]() 個單位長度,并把圖象上所有點的橫坐標縮短為原來的
個單位長度,并把圖象上所有點的橫坐標縮短為原來的![]() (縱坐標不變),得到
(縱坐標不變),得到![]() 的圖象.若
的圖象.若![]() 圖象的一個對稱中心為
圖象的一個對稱中心為![]() ,求
,求![]() 的最小值;
的最小值;
(3)在(2)條件下,求![]() 在
在![]() 上的增區間.
上的增區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com