
【題目】已知函數(shù)![]() .
.
(Ⅰ)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的極值;
的極值;
(Ⅱ)![]()
![]() 時,討論
時,討論![]() 的單調(diào)性;
的單調(diào)性;
(Ⅲ)若對任意的![]() 恒有
恒有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)函數(shù)![]() 的極小值為
的極小值為![]() ,無極大值;(Ⅱ)當
,無極大值;(Ⅱ)當![]() 時,函數(shù)
時,函數(shù)![]() 的在定義域
的在定義域![]() 單調(diào)遞增;當
單調(diào)遞增;當![]() 時,在區(qū)間
時,在區(qū)間![]() ,
,![]() 上
上![]() 單調(diào)遞減,在區(qū)間
單調(diào)遞減,在區(qū)間![]() 上
上![]() 單調(diào)遞增;當
單調(diào)遞增;當![]() 時,在區(qū)間
時,在區(qū)間![]() ,
,![]() 上
上![]() 單調(diào)遞減,在區(qū)間
單調(diào)遞減,在區(qū)間![]() ,上
,上![]() 單調(diào)遞增.
單調(diào)遞增.
(Ⅲ)![]() .
.
【解析】
試題(1)函數(shù)![]() 的定義域為
的定義域為![]() , 當
, 當![]() 時,函數(shù)
時,函數(shù)![]() ,利用導函數(shù)求出函數(shù)
,利用導函數(shù)求出函數(shù)![]() 的單調(diào)性,即可求出函數(shù)
的單調(diào)性,即可求出函數(shù)![]() 的極值;
的極值;
(2)由![]() ,所以
,所以![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,對
,對![]() 、
、![]() 、
、![]() 分類討論,求出
分類討論,求出![]() 的單調(diào)性;
的單調(diào)性;
(3)若對任意的![]()
![]() 恒有
恒有![]() 成立,等價于當
成立,等價于當![]() ,對任意的
,對任意的![]() ,恒有
,恒有![]() 成立,由(Ⅱ)知
成立,由(Ⅱ)知![]() ,
,![]() ,所以上式化為對任意的
,所以上式化為對任意的![]() ,恒有
,恒有![]() 成立,即
成立,即![]() ,因為
,因為![]() ,所以
,所以![]() ,所以
,所以![]() .
.
試題解析:(1)函數(shù)![]() 的定義域為
的定義域為![]() .
.![]() ,令
,令![]() ,
,
得![]() ;
;![]() (舍去).
(舍去).
當![]() 變化時,
變化時,![]() 的取值情況如下:
的取值情況如下:
|
|
|
|
| — | 0 |
|
| 減 | 極小值 | 增 |
所以,函數(shù)![]() 的極小值為
的極小值為![]() ,無極大值.
,無極大值.
(2)![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 的在定義域
的在定義域![]() 單調(diào)遞減;
單調(diào)遞減;
當![]() 時,在區(qū)間
時,在區(qū)間![]() ,
,![]() ,上
,上![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
在區(qū)間![]() ,上
,上![]() ,
,![]() 單調(diào)遞增;
單調(diào)遞增;
當![]() 時,在區(qū)間
時,在區(qū)間![]() ,
,![]() ,上
,上![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
在區(qū)間![]() ,上
,上![]() ,
,![]() 單調(diào)遞增.
單調(diào)遞增.
(3)由(2)知當![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞減;所以,當
單調(diào)遞減;所以,當![]() 時,
時,![]() ,
,![]()
問題等價于:對任意的![]() ,恒有
,恒有![]() 成立,即
成立,即![]() ,因為a<0,
,因為a<0,![]() ,
,![]() 所以,實數(shù)
所以,實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數(shù)學 來源: 題型:
【題目】為了普及環(huán)保知識,增強環(huán)保意識,某大學從理工類專業(yè)的![]() 班和文史類專業(yè)的
班和文史類專業(yè)的![]() 班各抽取
班各抽取![]() 名同學參加環(huán)保知識測試,統(tǒng)計得到成績與專業(yè)的列聯(lián)表:( )
名同學參加環(huán)保知識測試,統(tǒng)計得到成績與專業(yè)的列聯(lián)表:( )
優(yōu)秀 | 非優(yōu)秀 | 總計 | |
| 14 | 6 | 20 |
| 7 | 13 | 20 |
總計 | 21 | 19 | 40 |
附:參考公式及數(shù)據(jù):
(1)統(tǒng)計量:![]() ,(
,(![]() ).
).
(2)獨立性檢驗的臨界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
則下列說法正確的是
A. 有![]() 的把握認為環(huán)保知識測試成績與專業(yè)有關
的把握認為環(huán)保知識測試成績與專業(yè)有關
B. 有![]() 的把握認為環(huán)保知識測試成績與專業(yè)無關
的把握認為環(huán)保知識測試成績與專業(yè)無關
C. 有![]() 的把握認為環(huán)保知識測試成績與專業(yè)有關
的把握認為環(huán)保知識測試成績與專業(yè)有關
D. 有![]() 的把握認為環(huán)保知識測試成績與專業(yè)無關
的把握認為環(huán)保知識測試成績與專業(yè)無關
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知雙曲線![]() (a>0,b>0)的右焦點為F(3,0),左、右頂點分別為M,N,點P是E在第一象限上的任意一點,且滿足kPMkPN=8.
(a>0,b>0)的右焦點為F(3,0),左、右頂點分別為M,N,點P是E在第一象限上的任意一點,且滿足kPMkPN=8.
(1)求雙曲線E的方程;
(2)若直線PN與雙曲線E的漸近線在第四象限的交點為A,且△PAF的面積不小于3![]() ,求直線PN的斜率k的取值范圍.
,求直線PN的斜率k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列說法正確的是( )
A.命題p:![]() ,則¬p:x∈R,x2+x+1<0
,則¬p:x∈R,x2+x+1<0
B.在△ABC中,“A<B”是“sinA<sinB”的既不充分也不必要條件
C.若命題p∧q為假命題,則p,q都是假命題
D.命題“若x2﹣3x+2=0,則x=1”的逆否命題為“x≠1,則x2﹣3x+2≠0”
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題中正確的是( )
A.若p∨q為真命題,則p∧q為真命題
B.“x=5”是“x2-4x-5=0”的充分不必要條件
C.命題“若x<-1,則x2-2x-3>0”的否定為:“若x≥-1,則x2-2x-3≤0”
D.已知命題p:x∈R,x2+x-1<0,則![]() p:x∈R,x2+x-1≥0
p:x∈R,x2+x-1≥0
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】橢圓![]() 將圓
將圓![]() 的圓周分為四等份,且橢圓
的圓周分為四等份,且橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,且
,且![]() 的中點為
的中點為![]() ,線段
,線段![]() 的垂直平分線為
的垂直平分線為![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,已知橢圓的長軸為
的左、右焦點,已知橢圓的長軸為![]() 是橢圓
是橢圓![]() 上一動點,
上一動點,![]() 的最大值為
的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,
兩點,![]() 為橢圓
為橢圓![]() 上一點,
上一點,![]() 為坐標原點,且滿足
為坐標原點,且滿足![]() ,其中
,其中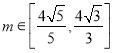 ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com