
【題目】已知常數![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,
, ![]() ,
, ![]() ;
;
(1)求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,且
,且![]() 是單調遞增數列,求實數
是單調遞增數列,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() ,
, ![]() ,對于任意給定的正整數
,對于任意給定的正整數![]() ,是否存在正整數
,是否存在正整數![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要寫出一組即可);若不存在,請說明理由;
的值(只要寫出一組即可);若不存在,請說明理由;
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]() ,
, ![]() (或
(或![]() ,
, ![]() ;…)
;…)
【解析】試題分析:(1)將條件![]() 中分式變成整式得
中分式變成整式得![]() ,把
,把![]() 換成
換成![]() 得
得![]() ,兩式相減化簡可得
,兩式相減化簡可得![]() ,化簡得
,化簡得![]() ,根據等差數列定義可知數列
,根據等差數列定義可知數列![]() 為等差數列,由等差數列通項公式寫出公式即可。(2)由(1)可得
為等差數列,由等差數列通項公式寫出公式即可。(2)由(1)可得![]() ,因為數列
,因為數列![]() 是單調遞增數列,所以
是單調遞增數列,所以![]() ,
, ![]() ,化簡得
,化簡得![]() ,因為
,因為![]() 的正負與
的正負與![]() 是奇數、偶數有關,故分兩種情況討論。當
是奇數、偶數有關,故分兩種情況討論。當![]() 是奇數時,
是奇數時, ![]() 可變為
可變為![]() 恒成立,構造函數求不等式右邊的最大值,令
恒成立,構造函數求不等式右邊的最大值,令![]() ,用函數單調性定義可證明單調性為減函數,所以
,用函數單調性定義可證明單調性為減函數,所以![]() ;當
;當![]() 是偶數時,
是偶數時, ![]() 可變為
可變為![]() 恒成立,構造函數求不等式右邊的最小值,令
恒成立,構造函數求不等式右邊的最小值,令![]() ,利用函數單調性定義證明函數為增函數,所以
,利用函數單調性定義證明函數為增函數,所以![]() 。可得所求范圍。(3)由(1)及
。可得所求范圍。(3)由(1)及![]() 可求出
可求出![]() ,所以
,所以 ![]() 。假設對任意
。假設對任意![]() ,總存在正整數
,總存在正整數![]() ,使
,使![]() ,可得關于
,可得關于![]() 的關系式
的關系式 ![]() 整理可得
整理可得![]() ,給出
,給出![]() 的值,可求出
的值,可求出![]() 的值。
的值。
試題解析:解:(1) ![]()
![]()
∴![]() 是以
是以![]() 為首項,
為首項, ![]() 為公差的等差數列,∴
為公差的等差數列,∴![]()
(2) ![]() ,即
,即![]()
若![]() 為奇數,則
為奇數,則![]() 恒成立,
恒成立,
考察![]() ,
, 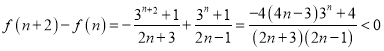
即![]() ,∴
,∴![]() ;
;
若![]() 為偶數,則
為偶數,則![]() 恒成立,
恒成立,
考察![]() ,
, 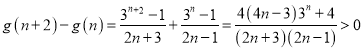
即![]() ,∴
,∴![]() ;綜上所述,
;綜上所述, ![]() ;
;
(3)由(1) ![]() .假設對任意
.假設對任意![]() ,總存在正整數
,總存在正整數![]() ,使
,使![]() ,
,
則![]()
令![]() ,則
,則![]() (或
(或![]() ,則
,則![]() ;…)
;…)
∴![]() (或
(或![]() ;…)
;…)


 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】已知雙曲正弦函數shx= ![]() 和雙曲余弦函數chx=
和雙曲余弦函數chx= ![]() 與我們學過的正弦函數和余弦函數有許多類似的性質,請類比正弦函數和余弦函數的和角公式,寫出雙曲正弦或雙曲余弦函數的一個類似的正確結論 .
與我們學過的正弦函數和余弦函數有許多類似的性質,請類比正弦函數和余弦函數的和角公式,寫出雙曲正弦或雙曲余弦函數的一個類似的正確結論 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將邊長為![]() 的等邊
的等邊![]() 沿
沿![]() 軸正方向滾動,某時刻
軸正方向滾動,某時刻![]() 與坐標原點重合(如圖),設頂點
與坐標原點重合(如圖),設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,關于函數
,關于函數![]() 有下列說法:
有下列說法:

(1)![]() 的值域為
的值域為![]() ;
;
(2)![]() 是周期函數且周期為
是周期函數且周期為![]() ;
;
(3)![]() ;
;
(4)滾動后,當頂點![]() 第一次落在
第一次落在![]() 軸上時,
軸上時,![]() 的圖象與
的圖象與![]() 軸所圍成的面積為
軸所圍成的面積為![]()
其中正確命題的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,且當x≥0時,f(x)=x|x﹣2|.若關于x的方程f2(x)+af(x)+b=0(a,b∈R)恰有10個不同實數解,則a的取值范圍為( )
A.(0,2)
B.(﹣2,0)
C.(1,2)
D.(﹣2,﹣1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是由
是由![]() 個有序實數構成的一個數組,記作
個有序實數構成的一個數組,記作![]() ,其中
,其中![]()
![]()
![]() 稱為數組
稱為數組![]() 的“元”,
的“元”, ![]() 稱為
稱為![]() 的下標,如果數組
的下標,如果數組![]() 中的每個“元”都是來自數組
中的每個“元”都是來自數組
![]() 中不同下標的“元”,則稱
中不同下標的“元”,則稱![]() 為
為![]() 的子數組,定義兩個數組
的子數組,定義兩個數組![]() 和
和![]()
![]() 的關系數為
的關系數為![]() ;
;
(1)若![]() ,
, ![]() ,設
,設![]() 是
是![]() 的含有兩個“元”的子數組,求
的含有兩個“元”的子數組,求![]()
的最大值;
(2)若 ,
, ![]() ,且
,且![]() ,
, ![]() 為
為![]() 的含有三個“元”
的含有三個“元”
的子數組,求![]() 的最大值;
的最大值;
(3)若數組![]() 中的“元”滿足
中的“元”滿足![]() ,設數組
,設數組![]()
![]() 含有
含有
四個“元”![]() ,且
,且![]() ,求
,求![]() 與
與![]() 的所有含有三個“元”
的所有含有三個“元”
的子數組的關系數的最大值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,k),
=(sinx,k), ![]() =(﹣2cosx,sinx﹣k).
=(﹣2cosx,sinx﹣k).
(1)當x∈[0, ![]() ]時,求|
]時,求| ![]() +
+ ![]() |的取值范圍;
|的取值范圍;
(2)若g(x)=( ![]() +
+ ![]() )
) ![]() ,求當k為何值時,g(x)的最小值為﹣
,求當k為何值時,g(x)的最小值為﹣ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
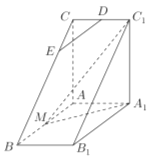
【題目】如圖,直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點,△
的中點,△![]() 是等腰三角形,
是等腰三角形, ![]() 為
為![]() 的中點,
的中點, ![]() 為
為![]() 上一點;
上一點;
(1)若![]() ∥平面
∥平面![]() ,求
,求![]() ;
;
(2)平面![]() 將三棱柱
將三棱柱![]() 分成兩個部分,求含有點
分成兩個部分,求含有點![]() 的那部分體積;
的那部分體積;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別為△ABC三個內角A,B,C所對的邊長,且acosB+bcosA=2ccosC.
(1)求角C的值;
(2)若c=4,a+b=7,求S△ABC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C1:x2+y2=4與圓C2:(x﹣1)2+(y﹣3)2=4,過動點P(a,b)分別作圓C1、圓C2的切線PM,PN,(M,N分別為切點),若|PM|=|PN|,則a2+b2﹣6a﹣4b+13的最小值是( )
A.5
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com