
【題目】如圖,在梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,又
,又![]() 平面
平面![]() ,
,![]() .
.

求:(1)二面角![]() 的大小(用反三角函數(shù)表示);
的大小(用反三角函數(shù)表示);
(2)點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)過A作![]() ,連接PE,根據(jù)
,連接PE,根據(jù)![]() 平面
平面![]() ,得到
,得到![]() ,由線面垂直的判定定理得到
,由線面垂直的判定定理得到![]() 平面
平面![]() ,從而
,從而![]() 二面角
二面角![]() 的平面角,然后根據(jù)
的平面角,然后根據(jù)![]() 求得
求得![]() ,再利用
,再利用![]() 求解.
求解.
(2)過A作![]() ,根據(jù)
,根據(jù)![]() ,得到
,得到![]() ,易得
,易得![]() ,從而得到
,從而得到![]() 平面
平面![]() ,由面面垂直的判定定理可得
,由面面垂直的判定定理可得![]() 平面
平面![]() ,得到
,得到![]() 平面
平面![]() ,即
,即![]() 為點(diǎn)
為點(diǎn)![]() 到平面
到平面![]() 的距離,然后在
的距離,然后在![]() 中求解.
中求解.
(1)如圖所示:
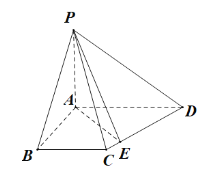
過A作![]() ,連接PE,
,連接PE,
因?yàn)?/span>![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() ,又
,又![]()
所以![]() 平面
平面![]() ,
,
所以![]() 二面角
二面角![]() 的平面角,
的平面角,
因?yàn)?/span>![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
即二面角![]() 的大小
的大小![]() .
.
(2)如圖所示:
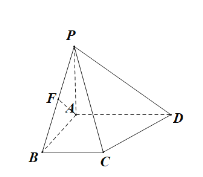
過A作![]() ,
,
因?yàn)?/span>![]() ,
,
所以![]()
因?yàn)?/span>![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() ,又
,又![]()
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又平面
,又平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 為點(diǎn)
為點(diǎn)![]() 到平面
到平面![]() 的距離,
的距離,
在![]() 中,
中,![]() .
.
所以點(diǎn)![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=x2-(a+2)x+alnx(a∈R).
(1)求函數(shù)f(x)的單調(diào)區(qū)間;
(2)若a=4,y=f(x)的圖象與直線y=m有三個交點(diǎn),求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在一次購物抽獎活動中,假設(shè)10張獎券中有一等獎獎券1張,可獲價值50元的獎品,有二等獎獎券3張,每張可獲價值10元的獎品,其余6張沒有獎品.
(1)顧客甲從10張獎券中任意抽取1張,求中獎次數(shù)X的概率分布;
(2)顧客乙從10張獎券中任意抽取2張,
①求顧客乙中獎的概率;
②設(shè)顧客乙獲得的獎品總價值Y元,求Y的概率分布及期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某車間租賃甲、乙兩種設(shè)備生產(chǎn)A,B兩類產(chǎn)品,甲種設(shè)備每天能生產(chǎn)A類產(chǎn)品8件和B類產(chǎn)品15件,乙種設(shè)備每天能生產(chǎn)A類產(chǎn)品10件和B類產(chǎn)品25件,已知設(shè)備甲每天的租賃費(fèi)300元,設(shè)備乙每天的租賃費(fèi)400元,現(xiàn)車間至少要生產(chǎn)A類產(chǎn)品100件,B類產(chǎn)品200件,所需租賃費(fèi)最少為__元![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在5月6日返校體檢中,學(xué)號為![]() (
(![]() )的五位同學(xué)的體重增加量
)的五位同學(xué)的體重增加量![]() 是集合
是集合![]() 中的元素,并滿足
中的元素,并滿足![]() ,則這五位同學(xué)的體重增加量所有可能的情況有________種
,則這五位同學(xué)的體重增加量所有可能的情況有________種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)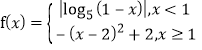 ,則方程
,則方程![]() (
(![]() )的實(shí)數(shù)根個數(shù)不可能為( )
)的實(shí)數(shù)根個數(shù)不可能為( )
A. 5個 B. 6個 C. 7個 D. 8個
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過拋物線y2=8x的焦點(diǎn),作傾斜角為45°的直線,則被拋物線截得的弦長為( )
A. 8 B. 16 C. 32 D. 64
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列判斷中正確的是( )
A. “若![]() ,則
,則![]() 有實(shí)數(shù)根”的逆否命題是假命題
有實(shí)數(shù)根”的逆否命題是假命題
B. “![]() ”是“直線
”是“直線![]() 與直線
與直線![]() 平行”的充要條件
平行”的充要條件
C. 命題“![]() ”是真命題
”是真命題
D. 已知命題![]() ,使得
,使得![]() ;命題
;命題![]() ,則
,則![]() 是真命題.
是真命題.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com