
【題目】某汽車公司為調查4S店個數對該公司汽車銷量的影響,對同等規模的A,B,C,D四座城市的4S店一個月某型號汽車銷量進行了統計,結果如下表:
城市 | A | B | C | D |
4S店個數x | 3 | 4 | 6 | 7 |
銷售臺數y | 18 | 26 | 34 | 42 |
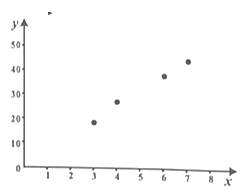
(1)由散點圖知y與x具有線性相關關系,求y關于x的線性回歸方程;
(2)根據統計每個城市汽車的盈利![]() (萬元)與該城市4S店的個數x符合函數
(萬元)與該城市4S店的個數x符合函數![]() ,
,![]() ,為擴大銷售,該公司在同等規模的城市E預計要開設多少個4S店,才能使E市的4S店一個月某型號騎車銷售盈利達到最大,并求出最大值.
,為擴大銷售,該公司在同等規模的城市E預計要開設多少個4S店,才能使E市的4S店一個月某型號騎車銷售盈利達到最大,并求出最大值.
附:回歸方程![]() 中的斜率和截距的最小二乘法估計公式分別為:
中的斜率和截距的最小二乘法估計公式分別為: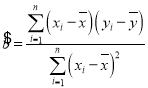 ,
,![]()
科目:高中數學 來源: 題型:
【題目】某校為了普及環保知識,增強學生的環保意識,在全校組織了一次有關環保知識的競賽.經過初賽、復賽,甲、乙兩個代表隊(每隊3人)進入了決賽,規定每人回答一個問題,答對為本隊贏得10分,答錯得0分.假設甲隊中每人答對的概率均為![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為![]() ,
,![]() ,
,![]() ,且各人回答正確與否相互之間沒有影響,用
,且各人回答正確與否相互之間沒有影響,用![]() 表示乙隊的總得分.
表示乙隊的總得分.
(Ⅰ)求![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅱ)求甲、乙兩隊總得分之和等于30分且甲隊獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某單位甲、乙、丙三個部門的員工人數分別為24,16,16.現采用分層抽樣的方法從中抽取7人,進行睡眠時間的調查.
(I)應從甲、乙、丙三個部門的員工中分別抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,現從這7人中隨機抽取3人做進一步的身體檢查.
(i)用X表示抽取的3人中睡眠不足的員工人數,求隨機變量X的分布列與數學期望;
(ii)設A為事件“抽取的3人中,既有睡眠充足的員工,也有睡眠不足的員工”,求事件A發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某“雙一流”大學專業獎學金是以所學專業各科考試成績作為評選依據,分為專業一等獎學金(獎金額![]() 元)、專業二等獎學金(獎金額
元)、專業二等獎學金(獎金額![]() 元)及專業三等獎學金(獎金額
元)及專業三等獎學金(獎金額![]() 元),且專業獎學金每個學生一年最多只能獲得一次.圖(1)是統計了該校
元),且專業獎學金每個學生一年最多只能獲得一次.圖(1)是統計了該校![]() 年
年![]() 名學生周課外平均學習時間頻率分布直方圖,圖(2)是這
名學生周課外平均學習時間頻率分布直方圖,圖(2)是這![]() 名學生在
名學生在![]() 年周課外平均學習時間段獲得專業獎學金的頻率柱狀圖.
年周課外平均學習時間段獲得專業獎學金的頻率柱狀圖.
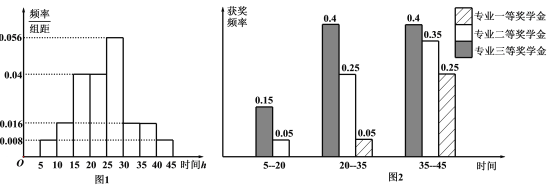
(Ⅰ)求這![]() 名學生中獲得專業三等獎學金的人數;
名學生中獲得專業三等獎學金的人數;
(Ⅱ)若周課外平均學習時間超過![]() 小時稱為“努力型”學生,否則稱為“非努力型”學生,列
小時稱為“努力型”學生,否則稱為“非努力型”學生,列![]() 聯表并判斷是否有
聯表并判斷是否有![]() 的把握認為該校學生獲得專業一、二等獎學金與是否是“努力型”學生有關?
的把握認為該校學生獲得專業一、二等獎學金與是否是“努力型”學生有關?
(Ⅲ)若以頻率作為概率,從該校任選一名學生,記該學生![]() 年獲得的專業獎學金額為隨機變量
年獲得的專業獎學金額為隨機變量![]() ,求隨機變量
,求隨機變量![]() 的分布列和期望.
的分布列和期望.
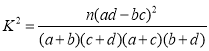
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題:
①“若![]() ,則
,則![]() ”的逆否命題為真命題
”的逆否命題為真命題
②“![]() ”是“函數
”是“函數![]() 在區間
在區間![]() 上為增函數”的充分不必要條件
上為增函數”的充分不必要條件
③若![]() 為假命題,則
為假命題,則![]() ,
,![]() 均為假命題
均為假命題
④對于命題![]() :
:![]() ,
,![]() ,則
,則![]() 為:
為:![]() ,
,![]()
其中真命題的個數是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交通指數是指交通擁堵指數的簡稱,是綜合反映道路網暢通或擁堵的概念性指數值,記交通指數為![]() ,其范圍為
,其范圍為![]() ,分別有五個級別:
,分別有五個級別:![]() ,暢通;
,暢通;![]() ,基本暢通;
,基本暢通;![]() ,輕度擁堵;
,輕度擁堵;![]() ,中度擁堵;
,中度擁堵;![]() ,嚴重擁堵.在晚高峰時段(
,嚴重擁堵.在晚高峰時段(![]() ),從某市交通指揮中心選取了市區20個交通路段,依據其交通指數數據繪制的頻率分布直方圖如圖所示.
),從某市交通指揮中心選取了市區20個交通路段,依據其交通指數數據繪制的頻率分布直方圖如圖所示.

(1)求出輕度擁堵、中度擁堵、嚴重擁堵的路段的個數;
(2)用分層抽樣的方法從輕度擁堵、中度擁堵、嚴重擁堵的路段中共抽取6個路段,求依次抽取的三個級別路段的個數;
(3)從(2)中抽取的6個路段中任取2個,求至少有1個路段為輕度擁堵的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 中點,
中點,![]() .
.
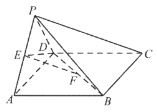
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 平面
平面![]() ?若存在,指出點
?若存在,指出點![]() 的位置;若不存在,說明理由.
的位置;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com