
【題目】某校為了普及環保知識,增強學生的環保意識,在全校組織了一次有關環保知識的競賽.經過初賽、復賽,甲、乙兩個代表隊(每隊3人)進入了決賽,規定每人回答一個問題,答對為本隊贏得10分,答錯得0分.假設甲隊中每人答對的概率均為![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為![]() ,
,![]() ,
,![]() ,且各人回答正確與否相互之間沒有影響,用
,且各人回答正確與否相互之間沒有影響,用![]() 表示乙隊的總得分.
表示乙隊的總得分.
(Ⅰ)求![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅱ)求甲、乙兩隊總得分之和等于30分且甲隊獲勝的概率.
科目:高中數學 來源: 題型:
【題目】某區的區人大代表有教師6 人,分別來自甲、乙、丙、丁四個學校,其中甲校教師記為![]() ,
,![]() ,乙校教師記為
,乙校教師記為![]() ,
,![]() ,丙校教師記為C,丁校教師記為D.現從這6 名教師代表中選出 3 名教師組成十九大報告宣講團,要求甲、乙、丙、丁四個學校中,每校至多選出1名.
,丙校教師記為C,丁校教師記為D.現從這6 名教師代表中選出 3 名教師組成十九大報告宣講團,要求甲、乙、丙、丁四個學校中,每校至多選出1名.
(1)請列出十九大報告宣講團組成人員的全部可能結果;
(2)求教師![]() 被選中的概率;
被選中的概率;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,直線
,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,且
,且![]() 是
是![]() 的中點.
的中點.
(Ⅰ)求橢圓的離心率;
(Ⅱ)過點![]() 的直線與橢圓相交于
的直線與橢圓相交于![]() 兩點,
兩點,![]() 都在
都在![]() 軸上方,并且
軸上方,并且![]() 在
在![]() 之間,且
之間,且![]() 到直線
到直線![]() 的距離是
的距離是![]() 到直線
到直線![]() 距離的
距離的![]() 倍.
倍.
①記![]() 的面積分別為
的面積分別為![]() ,求
,求![]() ;
;
②若原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求橢圓方程.
,求橢圓方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四校錐P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,邊長為4的正△PAD所在平面與平面ABCD垂直,點E是AD的中點,點Q是側棱PC的中點.

(1)求四棱錐P﹣ABCD的體積;
(2)求證:PA∥平面BDQ;
(3)在線段AB上是否存在點F,使直線PF與平面PAD所成的角為30°?若存在,求出AF的長,若不存在,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
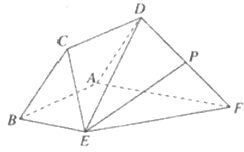
【題目】如圖,已知菱形![]() 與直角梯形
與直角梯形![]() 所在的平面互相垂直,其中
所在的平面互相垂直,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點
的中點
(Ⅰ)求證:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)設![]() 為線段
為線段![]() 上一點,
上一點,![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校學生社團組織活動豐富,學生會為了解同學對社團活動的滿意程度,隨機選取了100位同學進行問卷調查,并將問卷中的這100人根據其滿意度評分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6組,制成如圖所示頻率分布直方圖.
(1)求圖中x的值;
(2)求這組數據的中位數;
(3)現從被調查的問卷滿意度評分值在[60,80)的學生中按分層抽樣的方法抽取5人進行座談了解,再從這5人中隨機抽取2人作主題發言,求抽取的2人恰在同一組的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車公司為調查4S店個數對該公司汽車銷量的影響,對同等規模的A,B,C,D四座城市的4S店一個月某型號汽車銷量進行了統計,結果如下表:
城市 | A | B | C | D |
4S店個數x | 3 | 4 | 6 | 7 |
銷售臺數y | 18 | 26 | 34 | 42 |
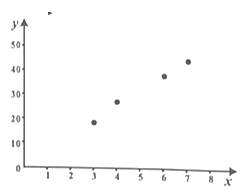
(1)由散點圖知y與x具有線性相關關系,求y關于x的線性回歸方程;
(2)根據統計每個城市汽車的盈利![]() (萬元)與該城市4S店的個數x符合函數
(萬元)與該城市4S店的個數x符合函數![]() ,
,![]() ,為擴大銷售,該公司在同等規模的城市E預計要開設多少個4S店,才能使E市的4S店一個月某型號騎車銷售盈利達到最大,并求出最大值.
,為擴大銷售,該公司在同等規模的城市E預計要開設多少個4S店,才能使E市的4S店一個月某型號騎車銷售盈利達到最大,并求出最大值.
附:回歸方程![]() 中的斜率和截距的最小二乘法估計公式分別為:
中的斜率和截距的最小二乘法估計公式分別為: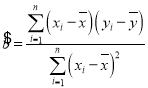 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
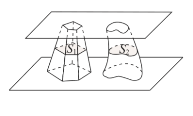
【題目】南北朝時代的偉大科學家祖暅在數學上有突出貢獻,他在實踐的基礎上提出祖暅原理:“冪勢既同,則積不容異”. 其含義是:夾在兩個平行平面之間的兩個幾何體,被平行于這兩個平行平面的任意平面所截,如果截得的兩個截面的面積總相等,那么這兩個幾何體的體積相等.如圖,夾在兩個平行平面之間的兩個幾何體的體積分別為![]() ,被平行于這兩個平面的任意平面截得的兩個截面面積分別為
,被平行于這兩個平面的任意平面截得的兩個截面面積分別為![]() ,則“
,則“![]() 相等”是“
相等”是“![]() 總相等”的
總相等”的
A. 充分而不必要條件B. 必要而不充分條件
C. 充分必要條件D. 既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com