
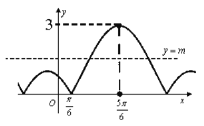
【題目】如圖是函數(shù)![]() 的部分圖象.
的部分圖象.

(1)求函數(shù)![]() 的表達(dá)式;
的表達(dá)式;
(2)若函數(shù)![]() 滿足方程
滿足方程![]() ,求在
,求在![]() 內(nèi)的所有實(shí)數(shù)根之和;
內(nèi)的所有實(shí)數(shù)根之和;
(3)把函數(shù)![]() 的圖象的周期擴(kuò)大為原來的兩倍,然后向右平移
的圖象的周期擴(kuò)大為原來的兩倍,然后向右平移![]() 個(gè)單位,再把縱坐標(biāo)伸長為原來的兩倍,最后向上平移一個(gè)單位得到函數(shù)
個(gè)單位,再把縱坐標(biāo)伸長為原來的兩倍,最后向上平移一個(gè)單位得到函數(shù)![]() 的圖象.若對任意的
的圖象.若對任意的![]() ,方程
,方程![]() 在區(qū)間
在區(qū)間![]() 上至多有一個(gè)解,求正數(shù)
上至多有一個(gè)解,求正數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)答案不唯一,具體見解析(3)
(2)答案不唯一,具體見解析(3)![]()
【解析】
(1)根據(jù)圖像先確定A,再確定![]() ,代入一個(gè)特殊點(diǎn)再確定
,代入一個(gè)特殊點(diǎn)再確定![]() 。
。
(2)根據(jù)(1)的結(jié)果結(jié)合圖像即可解決。
(3)根據(jù)(1)的結(jié)果以及三角函數(shù)的變換求出![]() 即可解決。
即可解決。
解:(Ⅰ)由圖可知:![]() ,即
,即![]() ,
,
![]() 又由圖可知:
又由圖可知:![]() 是五點(diǎn)作圖法中的第三點(diǎn),
是五點(diǎn)作圖法中的第三點(diǎn),
![]() ,即
,即![]() .
.
(Ⅱ)因?yàn)?/span>![]() 的周期為
的周期為![]() ,
,![]() 在
在![]() 內(nèi)恰有
內(nèi)恰有![]() 個(gè)周期.
個(gè)周期.
⑴當(dāng)![]() 時(shí),方程
時(shí),方程![]() 在
在![]() 內(nèi)有
內(nèi)有![]() 個(gè)實(shí)根,
個(gè)實(shí)根,
設(shè)為![]()
![]() ,結(jié)合圖像知
,結(jié)合圖像知![]()
![]() ,
,
故所有實(shí)數(shù)根之和為![]() ;
;
⑵當(dāng)![]() 時(shí),方程
時(shí),方程![]() 在
在![]() 內(nèi)有
內(nèi)有![]() 個(gè)實(shí)根為
個(gè)實(shí)根為![]() ,
,
故所有實(shí)數(shù)根之和為![]() ;
;
⑶當(dāng)![]() 時(shí),方程
時(shí),方程![]() 在
在![]() 內(nèi)有
內(nèi)有![]() 個(gè)實(shí)根,
個(gè)實(shí)根,
設(shè)為![]()
![]() ,結(jié)合圖像知
,結(jié)合圖像知![]()
![]() ,
,
故所有實(shí)數(shù)根之和為![]() ;
;
綜上:當(dāng)![]() 時(shí),方程
時(shí),方程![]() 所有實(shí)數(shù)根之和為
所有實(shí)數(shù)根之和為![]() ;
;
當(dāng)![]() 時(shí),方程
時(shí),方程![]() 所有實(shí)數(shù)根之和為
所有實(shí)數(shù)根之和為![]() ;
;
(Ⅲ)![]() ,
,
函數(shù)![]() 的圖象如圖所示:
的圖象如圖所示:
則當(dāng)![]() 圖象伸長為原來的
圖象伸長為原來的![]() 倍以上時(shí)符合題意,
倍以上時(shí)符合題意,
所以![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)P1(a1 , b1),P2(a2 , b2),…,Pn(an , bn)(n∈N*)都在函數(shù)y=![]() 的圖象上.
的圖象上.
(Ⅰ)若數(shù)列{bn}是等差數(shù)列,求證數(shù)列{an}為等比數(shù)列;
(Ⅱ)若數(shù)列{an}的前n項(xiàng)和為Sn=1﹣2﹣n , 過點(diǎn)Pn , Pn+1的直線與兩坐標(biāo)軸所圍成三角形面積為cn , 求使cn≤t對n∈N*恒成立的實(shí)數(shù)t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 處有一港口,兩艘海輪
處有一港口,兩艘海輪![]() 同時(shí)從港口
同時(shí)從港口![]() 處出發(fā)向正北方向勻速航行,海輪
處出發(fā)向正北方向勻速航行,海輪![]() 的航行速度為20海里/小時(shí),海輪
的航行速度為20海里/小時(shí),海輪![]() 的航行速度大于海輪
的航行速度大于海輪![]() .在港口
.在港口![]() 北偏東60°方向上的
北偏東60°方向上的![]() 處有一觀測站,1小時(shí)后在
處有一觀測站,1小時(shí)后在![]() 處測得與海輪
處測得與海輪![]() 的距離為30海里,且
的距離為30海里,且![]() 處對兩艘海輪
處對兩艘海輪![]() ,
,![]() 的視角為30°.
的視角為30°.

(1)求觀測站![]() 到港口
到港口![]() 的距離;
的距離;
(2)求海輪![]() 的航行速度.
的航行速度.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】使用支付寶和微信支付已經(jīng)成為廣大消費(fèi)者最主要的消費(fèi)支付方式,某超市通過統(tǒng)計(jì)發(fā)現(xiàn)一周內(nèi)超市每天的凈利潤![]() (萬元)與每天使用支付寶和微信支付的人數(shù)
(萬元)與每天使用支付寶和微信支付的人數(shù)![]() (千人)具有線性相關(guān)關(guān)系,并得到最近一周
(千人)具有線性相關(guān)關(guān)系,并得到最近一周![]() 的7組數(shù)據(jù)如下表,并依此作為決策依據(jù).
的7組數(shù)據(jù)如下表,并依此作為決策依據(jù).

(1)作出散點(diǎn)圖,并求出回歸方程![]() (
(![]() ,
,![]() 精確到
精確到![]() );
);

(2)超市為了刺激周一消費(fèi),擬在周一開展使用支付寶和微信支付隨機(jī)抽獎活動,總獎金7萬元.根據(jù)市場調(diào)查,抽獎活動能使使用支付寶和微信支付消費(fèi)人數(shù)增加7千人,試決策超市是否有必要開
展抽獎活動?
(3)超市管理層決定:從周一到周日,若第二天的凈利潤比前一天增長超過兩成,則對全體員工進(jìn)行獎勵,在(Ⅱ)的決策下,求全體員工連續(xù)兩天獲得獎勵的概率.
參考數(shù)據(jù): ![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某車間將10名技工平均分成甲、乙兩組加工某種零件,在單位時(shí)間內(nèi)每個(gè)技工加工的合格零件數(shù),按十位數(shù)字為莖,個(gè)位數(shù)字為葉得到的莖葉圖如圖所示.已知甲、乙兩組數(shù)據(jù)的平均數(shù)都為10.

(1)求![]() 的值;
的值;
(2)分別求出甲、乙兩組數(shù)據(jù)的方差![]() 和
和![]() ,并由此分析兩組技工的加工水平;
,并由此分析兩組技工的加工水平;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市通過隨機(jī)詢問100名不同年級的學(xué)生是否能做到“扶跌倒老人”,得到如下列聯(lián)表:
做不到 | 能做到 | |
高年級 | 45 | 10 |
低年級 | 30 | 15 |
則下列結(jié)論正確的是( )
附參照表:
| 0.10 | 0.025 | 0.01 |
| 2.706 | 5.024 | 6.635 |
參考公式:![]() ,其中
,其中![]()
A. 在犯錯(cuò)誤的概率不超過![]() 的前提下,認(rèn)為“學(xué)生能否做到‘扶跌倒老人’與年級高低有關(guān)”
的前提下,認(rèn)為“學(xué)生能否做到‘扶跌倒老人’與年級高低有關(guān)”
B. 在犯錯(cuò)誤的概率不超過![]() 的前提下,“學(xué)生能否做到‘扶跌倒老人’與年級高低無關(guān)”
的前提下,“學(xué)生能否做到‘扶跌倒老人’與年級高低無關(guān)”
C. 有![]() 以上的把握認(rèn)為“學(xué)生能否做到‘扶跌倒老人’與年級高低有關(guān)”
以上的把握認(rèn)為“學(xué)生能否做到‘扶跌倒老人’與年級高低有關(guān)”
D. 有![]() 以上的把握認(rèn)為“學(xué)生能否做到‘扶跌倒老人’與年級高低無關(guān)”
以上的把握認(rèn)為“學(xué)生能否做到‘扶跌倒老人’與年級高低無關(guān)”
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)已知命題![]() :實(shí)數(shù)
:實(shí)數(shù)![]() 滿足
滿足![]() ,命題
,命題![]() :實(shí)數(shù)
:實(shí)數(shù)![]() 滿足方程
滿足方程![]() 表示的焦點(diǎn)在
表示的焦點(diǎn)在![]() 軸上的橢圓,且
軸上的橢圓,且![]() 是
是![]() 的充分不必要條件,求實(shí)數(shù)
的充分不必要條件,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)命題![]() :關(guān)于
:關(guān)于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ;
;![]() :函數(shù)
:函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() .若
.若![]() 是真命題,
是真命題,![]() 是假命題,求實(shí)數(shù)
是假命題,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校藝術(shù)節(jié)對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項(xiàng)參賽作品,只評一項(xiàng)一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學(xué)對這四項(xiàng)參賽作品預(yù)測如下:
四項(xiàng)參賽作品,只評一項(xiàng)一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學(xué)對這四項(xiàng)參賽作品預(yù)測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項(xiàng)作品未獲得一等獎”;
兩項(xiàng)作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學(xué)中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com