
【題目】已知點P1(a1 , b1),P2(a2 , b2),…,Pn(an , bn)(n∈N*)都在函數y=![]() 的圖象上.
的圖象上.
(Ⅰ)若數列{bn}是等差數列,求證數列{an}為等比數列;
(Ⅱ)若數列{an}的前n項和為Sn=1﹣2﹣n , 過點Pn , Pn+1的直線與兩坐標軸所圍成三角形面積為cn , 求使cn≤t對n∈N*恒成立的實數t的取值范圍.
【答案】解:(1)依題意可知bn=![]() an ,
an ,
∵數列{bn}是等差數列,
∴2bn+1=bn+bn+2 , 即2![]() an+1=
an+1=![]() an+
an+![]() an+2=
an+2=![]() (anan+2)
(anan+2)
∴a2n+1=anan+2
∴數列{an}為等比數列
(2)當n=1時,a1=![]() ,當n≥2時,an=Sn﹣Sn﹣1=(
,當n≥2時,an=Sn﹣Sn﹣1=(![]() )n , n=1也適合此式,
)n , n=1也適合此式,
即數列{an}的通項公式是an=(![]() )n . 由bn=
)n . 由bn=![]() an , 得
an , 得
數列{bn}的通項公式是bn=n,
所以Pn(![]() ,n),Pn+1(
,n),Pn+1(![]() ,n+1).
,n+1).
過這兩點的直線方程是:![]() =
=
可得與坐標軸的交點是An(![]() ,0),Bn(0,n+2),
,0),Bn(0,n+2),
cn=![]() ×|OAn|×|OBn|=
×|OAn|×|OBn|=![]() ,
,
由于cn﹣cn+1=![]() ﹣
﹣![]() >0,即數列{cn}的各項依次單調遞減,所以t≥c1=
>0,即數列{cn}的各項依次單調遞減,所以t≥c1=![]() ,即存在最小的實數t=
,即存在最小的實數t=![]() 滿足條件.
滿足條件.
【解析】(1)把點Pn(an , bn)代入函數式,根據數列{bn}是等差數列,可求得a2n+1=anan+1進而可證明數列an}為等比數列
(2)先看當n≥2時根據an=Sn﹣Sn﹣1求得數列{an}的通項公式,進而求得當n=1時也符合,求得數列{an}的通項公式代入bn=![]() an求得bn , 進而求得點Pn和Pn+1的坐標進而可得過這兩點的直線方程,進而求得該直線與坐標軸的交點坐標,根據三角形的面積公式求得cn , 進而可得cn﹣cn+1的表達式判斷其大于0,推斷出數列{cn}的各項依次單調遞減,要使cn≤t對n∈N+恒成立,需要t大于或等于數列的最大值c1 , 進而可推斷存在最小的實數滿足條件.
an求得bn , 進而求得點Pn和Pn+1的坐標進而可得過這兩點的直線方程,進而求得該直線與坐標軸的交點坐標,根據三角形的面積公式求得cn , 進而可得cn﹣cn+1的表達式判斷其大于0,推斷出數列{cn}的各項依次單調遞減,要使cn≤t對n∈N+恒成立,需要t大于或等于數列的最大值c1 , 進而可推斷存在最小的實數滿足條件.
【考點精析】通過靈活運用等比關系的確定和不等式的證明,掌握等比數列可以通過定義法、中項法、通項公式法、前n項和法進行判斷;不等式證明的幾種常用方法:常用方法有:比較法(作差,作商法)、綜合法、分析法;其它方法有:換元法、反證法、放縮法、構造法,函數單調性法,數學歸納法等即可以解答此題.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形,四邊形
為正方形,四邊形![]() 為梯形,且
為梯形,且![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,對角線
是菱形,對角線![]() ,
,![]() 交于點
交于點![]() .
.

(Ⅰ)若![]() ,求證:
,求證:![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,求證:
,求證:![]() ;
;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() (異于點
(異于點![]() ),使得
),使得![]() 平面
平面![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《史記》卷六十五《孫子吳起列傳第五》中有這樣一道題:齊王與田忌賽馬,田忌的上等馬優于齊王的中等馬,劣于齊王的上等馬,田忌的中等馬優于齊王的下等馬,劣于齊王的中等馬,田忌的下等馬劣于齊王的下等馬,現從雙方的馬匹中隨機選一匹馬進行一場比賽,齊王獲勝的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學將100名高一新生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A,B兩種不同的教學方式分別在甲、乙兩個班級進行教改實驗.為了解教學效果,期末考試后,陳老師分別從兩個班級中各隨機抽取20名學生的成績進行統計,作出莖葉圖如圖.記成績不低于90分者為“成績優秀”.

(1)在乙班樣本的20個個體中,從不低于86分的成績中隨機抽取2個,求抽出的2個均“成績優秀”的概率;
(2)由以上統計數據作出列聯表,并判斷能否在犯錯誤的概率不超過0.1的前提下認為:“成績優秀”與教學方式有關.
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
參考公式:![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】城市公交車的數量太多造成資源的浪費,太少又難以滿足乘客需求,為此,某市公交公司在某站臺的60名候車乘客中隨機抽取15名,將他們的候車時間(單位:分鐘)作為樣本分成5組,如下表所示:
組別 | 候車時間 | 人數 |
一 | [0,5) | 2 |
二 | [5,10) | 6 |
三 | [10,15) | 4 |
四 | [15,20) | 2 |
五 | [20,25] | 1 |
(1)求這15名乘客的平均候車時間
(2)估計這60名乘客候車時間少于10分鐘的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究機構對高三學生的記憶力![]() 和判斷力
和判斷力![]() 進行統計分析,得下表數據:
進行統計分析,得下表數據:
![]()
(1)請根據上表提供的數據,用相關系數![]() 說明
說明![]() 與
與![]() 的線性相關程度;(結果保留小數點后兩位,參考數據:
的線性相關程度;(結果保留小數點后兩位,參考數據: ![]() )
)
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)試根據求出的線性回歸方程,預測記憶力為9的同學的判斷力.
參考公式: ,
,![]() ;相關系數
;相關系數 ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取![]() 件,測量這些產品的一項質量指標值,由測量結果得如頻率分布直方圖:
件,測量這些產品的一項質量指標值,由測量結果得如頻率分布直方圖:
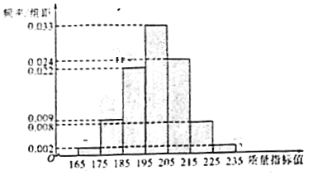
(1)求這![]() 件產品質量指標值的樣本平均數
件產品質量指標值的樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(2)由直方圖可以認為,這種產品的質量指標值![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
①利用該正態分布,求![]() ;
;
②某用戶從該企業購買了![]() 件這種產品,記
件這種產品,記![]() 表示這
表示這![]() 件產品中質量指標值位于區間
件產品中質量指標值位于區間![]() 的產品件數.利用①的結果,求
的產品件數.利用①的結果,求![]() .
.
附:![]() .若
.若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是函數![]() 的部分圖象.
的部分圖象.

(1)求函數![]() 的表達式;
的表達式;
(2)若函數![]() 滿足方程
滿足方程![]() ,求在
,求在![]() 內的所有實數根之和;
內的所有實數根之和;
(3)把函數![]() 的圖象的周期擴大為原來的兩倍,然后向右平移
的圖象的周期擴大為原來的兩倍,然后向右平移![]() 個單位,再把縱坐標伸長為原來的兩倍,最后向上平移一個單位得到函數
個單位,再把縱坐標伸長為原來的兩倍,最后向上平移一個單位得到函數![]() 的圖象.若對任意的
的圖象.若對任意的![]() ,方程
,方程![]() 在區間
在區間![]() 上至多有一個解,求正數
上至多有一個解,求正數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com