
(本小題滿分13分)
專家通過研究學(xué)生的學(xué)習(xí)行為,發(fā)現(xiàn)學(xué)生的注意力隨著老師講課時間的變化而變化,講課開始時,學(xué)生的興趣激增,中間有一段時間,學(xué)生的興趣保持較理想的狀態(tài),隨后學(xué)生的注意力開始分散,設(shè)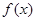 表示學(xué)生注意力隨時間
表示學(xué)生注意力隨時間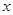 (分鐘)的變化規(guī)律(
(分鐘)的變化規(guī)律(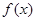 越大,表明學(xué)生注意力越大),經(jīng)過試驗分析得知:
越大,表明學(xué)生注意力越大),經(jīng)過試驗分析得知: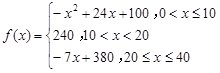
(Ⅰ)講課開始后多少分鐘,學(xué)生的注意力最集中?能堅持多少分鐘?
(Ⅱ)講課開始后5分鐘時與講課開始后25分鐘時比較,何時學(xué)生的注意力更集中?
(Ⅲ)一道數(shù)學(xué)難題,需要講解24分鐘,并且要求學(xué)生的注意力至少達到180,那么經(jīng)過適當(dāng)安排,老師能否在學(xué)生達到所需的狀態(tài)下講完這道題目?
(1) 堅持10分鐘(2) 學(xué)生的注意力比講課開始后5分鐘時更集中(3) 經(jīng)過適當(dāng)安排,老師能在學(xué)生達到所需的狀態(tài)下講完這道題目
解析試題分析:解:(Ⅰ)當(dāng)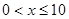 時,
時, 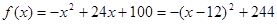 是增函數(shù),
是增函數(shù),
且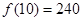
當(dāng)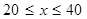 時,
時, 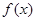 是減函數(shù),且
是減函數(shù),且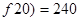
所以講課開始10分鐘,學(xué)生的注意力最集中,能堅持10分鐘. ………………………5分
(Ⅱ)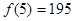 ,
,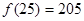 ,所以講課開始后25分鐘時,學(xué)生的注意力比講課開始后5分鐘時更集中. ……………8分
,所以講課開始后25分鐘時,學(xué)生的注意力比講課開始后5分鐘時更集中. ……………8分
(Ⅲ) 當(dāng)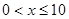 時,令
時,令 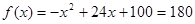 得
得 .
.
當(dāng)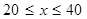 時令
時令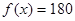 ,得
,得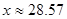
所以學(xué)生的注意力在180以上,所持續(xù)的時間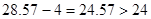
所以經(jīng)過適當(dāng)安排,老師能在學(xué)生達到所需的狀態(tài)下講完這道題目. …………………13分
考點:本試題考查了函數(shù)模型的運用。
點評:構(gòu)造二次函數(shù)模型,函數(shù)解析式求解是關(guān)鍵,解決實際問題通常有四個步驟:(1)閱讀理解,認真審題;(2)引進數(shù)學(xué)符號,建立數(shù)學(xué)模型;(3)利用數(shù)學(xué)的方法,得到數(shù)學(xué)結(jié)果;(4)轉(zhuǎn)譯成具體問題作出解答,其中關(guān)鍵是建立數(shù)學(xué)模型.


 應(yīng)用題作業(yè)本系列答案
應(yīng)用題作業(yè)本系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
水庫的蓄水量隨時間而變化,現(xiàn)用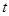 表示時間,以月為單位,年初為起點,根據(jù)歷年數(shù)據(jù),某水庫的蓄水量(單位:億立方米)關(guān)于
表示時間,以月為單位,年初為起點,根據(jù)歷年數(shù)據(jù),某水庫的蓄水量(單位:億立方米)關(guān)于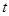 的近似函數(shù)關(guān)系式為:
的近似函數(shù)關(guān)系式為: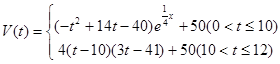
(1)該水庫的蓄水量小于50的時期稱為枯水期,以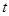 表示第
表示第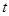 月份(
月份(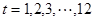 ),問:同一年內(nèi)哪些月份是枯水期?
),問:同一年內(nèi)哪些月份是枯水期?
(2)求一年內(nèi)哪個月份該水庫的蓄水量最大,并求最大蓄水量。(取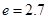 計算)
計算)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)設(shè)關(guān)于x的方程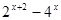
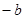 =0.
=0.
(Ⅰ) 如果b=1,求實數(shù)x的值;
(Ⅱ) 如果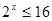 且
且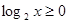 ,求實數(shù)b的取值范圍.
,求實數(shù)b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)南昌市在加大城市化進程中,環(huán)境污染問題也日益突出。據(jù)環(huán)保局測定,某處的污染指數(shù)與附近污染源的強度成正比,與到污染源距離的平方成反比.現(xiàn)已知相距18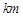 的A,B兩家工廠(視作污染源)的污染強度分別為
的A,B兩家工廠(視作污染源)的污染強度分別為 ,它們連線上任意一點C處的污染指數(shù)
,它們連線上任意一點C處的污染指數(shù) 等于兩家工廠對該處的污染指數(shù)之和.設(shè)
等于兩家工廠對該處的污染指數(shù)之和.設(shè) (
(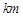 ).
).
(1) 試將 表示為
表示為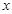 的函數(shù);
的函數(shù);
(2) 若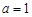 ,且
,且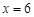 時,
時, 取得最小值,試求
取得最小值,試求 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
一變壓器的鐵芯截面為正十字型,為保證所需的磁通量,要求十字應(yīng)具有 的面積,問應(yīng)如何設(shè)計十字型寬
的面積,問應(yīng)如何設(shè)計十字型寬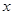 及長
及長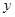 ,才能使其外接圓的周長最短,這樣可使繞在鐵芯上的銅線最節(jié)省.
,才能使其外接圓的周長最短,這樣可使繞在鐵芯上的銅線最節(jié)省.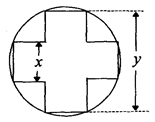
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)f(x)="2" sin (0≤x≤5),點A、B分別是函數(shù)y=f(x)圖像上的最高點和最低點.
(0≤x≤5),點A、B分別是函數(shù)y=f(x)圖像上的最高點和最低點.
(1)求點A、B的坐標(biāo)以及 ·
·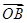 的值;
的值;
(2)沒點A、B分別在角 、
、 的終邊上,求tan(
的終邊上,求tan(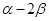 )的值.
)的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某工廠生產(chǎn)一種產(chǎn)品,已知該產(chǎn)品的月產(chǎn)量x噸與每噸產(chǎn)品的價格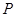 (元)之間的關(guān)系為
(元)之間的關(guān)系為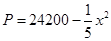 ,且生產(chǎn)
,且生產(chǎn) 噸的成本為
噸的成本為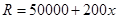 (元).問該廠每月生產(chǎn)多少噸產(chǎn)品才能使利潤達到最大?最大利潤是多少?(利潤=收入-成本)
(元).問該廠每月生產(chǎn)多少噸產(chǎn)品才能使利潤達到最大?最大利潤是多少?(利潤=收入-成本)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com