
已知函數f(x)="2" sin (0≤x≤5),點A、B分別是函數y=f(x)圖像上的最高點和最低點.
(0≤x≤5),點A、B分別是函數y=f(x)圖像上的最高點和最低點.
(1)求點A、B的坐標以及 ·
·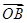 的值;
的值;
(2)沒點A、B分別在角 、
、 的終邊上,求tan(
的終邊上,求tan(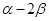 )的值.
)的值.
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某產品生產廠家根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品x(百臺),其總成本為G(x)(萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本).銷售收入R(x)(萬元)滿足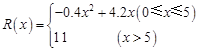 ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
(1)寫出利潤函數y=f(x)的解析式(利潤=銷售收入-總成本);
(2)工廠生產多少臺產品時,可使盈利最多?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
專家通過研究學生的學習行為,發現學生的注意力隨著老師講課時間的變化而變化,講課開始時,學生的興趣激增,中間有一段時間,學生的興趣保持較理想的狀態,隨后學生的注意力開始分散,設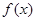 表示學生注意力隨時間
表示學生注意力隨時間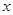 (分鐘)的變化規律(
(分鐘)的變化規律(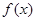 越大,表明學生注意力越大),經過試驗分析得知:
越大,表明學生注意力越大),經過試驗分析得知: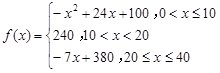
(Ⅰ)講課開始后多少分鐘,學生的注意力最集中?能堅持多少分鐘?
(Ⅱ)講課開始后5分鐘時與講課開始后25分鐘時比較,何時學生的注意力更集中?
(Ⅲ)一道數學難題,需要講解24分鐘,并且要求學生的注意力至少達到180,那么經過適當安排,老師能否在學生達到所需的狀態下講完這道題目?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分16分)
已知 ,
,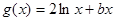 ,且直線
,且直線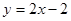 與曲線
與曲線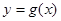 相切.
相切.
(1)若對 內的一切實數
內的一切實數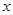 ,不等式
,不等式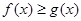 恒成立,求實數
恒成立,求實數 的取值范圍;
的取值范圍;
(2)當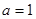 時,求最大的正整數
時,求最大的正整數 ,使得對
,使得對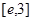 (
(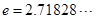 是自然對數的底數)內的任意
是自然對數的底數)內的任意 個實數
個實數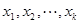 都有
都有 成立;
成立;
(3)求證: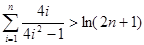
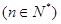 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
某廠生產某種零件,每個零件的成本為40元,出廠單價定為60元.該廠為鼓勵銷售商訂購,決定當一次訂購量超過100個時,每多訂購一個,訂購的全部零件的出廠單價就降低0.02元,但實際出廠單價不能低于51元.
(1)當一次訂購量為多少個時,零件的實際出廠單價恰降為51元?
(2)設一次訂購量為x個,零件的實際出廠單價為P元,寫出函數P=f(x)的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分10分)
一種放射性元素,最初的質量為500g,按每年10﹪衰減.
(Ⅰ)求t年后,這種放射性元素質量ω的表達式;
(Ⅱ)由求出的函數表達式,求這種放射性元素的半衰期(剩留量為原來的一半所需要的時間).(精確到0.1;參考數據: )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com