
【題目】某工廠的檢驗員為了檢測生產線上生產零件的情況,從產品中隨機抽取了![]() 個進行測量,根據所測量的數據畫出頻率分布直方圖如下:
個進行測量,根據所測量的數據畫出頻率分布直方圖如下:

如果:尺寸數據在![]() 內的零件為合格品,頻率作為概率.
內的零件為合格品,頻率作為概率.
(1)從產品中隨機抽取![]() 件,合格品的個數為
件,合格品的個數為![]() ,求
,求![]() 的分布列與期望:
的分布列與期望:
(2)為了提高產品合格率,現提出![]() ,
,![]() 兩種不同的改進方案進行試驗,若按
兩種不同的改進方案進行試驗,若按![]() 方案進行試驗后,隨機抽取
方案進行試驗后,隨機抽取![]() 件產品,不合格個數的期望是
件產品,不合格個數的期望是![]() :若按
:若按![]() 方案試驗后,抽取
方案試驗后,抽取![]() 件產品,不合格個數的期望是
件產品,不合格個數的期望是![]() ,你會選擇哪個改進方案?
,你會選擇哪個改進方案?
【答案】(1)詳見解析(2)應選擇方案![]() ,詳見解析
,詳見解析
【解析】
(1) 先由頻率分布直方圖,可以推出產品為合格品的概率,再求出隨機變量![]() 的分布列及期望;
的分布列及期望;
(2) ![]() 方案隨機抽取產品與
方案隨機抽取產品與![]() 方案隨機抽取產品都為相互獨立事件,服從二項分布,由不合格個數的期望分別求出不合格的概率即可得出較好的方案.
方案隨機抽取產品都為相互獨立事件,服從二項分布,由不合格個數的期望分別求出不合格的概率即可得出較好的方案.
(1)由直方圖可知抽出產品為合格品的率為![]()
即推出產品為合格品的概率為![]() ,
,
從產品中隨機抽取![]() 件.合格品的個數
件.合格品的個數![]() 的所有可能取值為0,1,2,3,4,
的所有可能取值為0,1,2,3,4,
且![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以![]() 的分布判為
的分布判為
|
|
|
|
|
|
|
|
|
|
|
|
![]() 的數學期望
的數學期望![]() .
.
(2)![]() 方案隨機抽取產品不合格的概率是
方案隨機抽取產品不合格的概率是![]() ,隨機抽取
,隨機抽取![]() 件產品,不合格個數
件產品,不合格個數![]() :
:
按![]() 方案隨機抽取產品不合格的概率是
方案隨機抽取產品不合格的概率是![]() ,隨機抽取
,隨機抽取![]() 件產品,不合格個數
件產品,不合格個數![]()
依題意![]() ,
,![]() ,
,
解得![]() ,
,![]()
因為![]() ,
,
所以應選擇方案![]() .
.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:高中數學 來源: 題型:
【題目】已知在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.
是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.

(Ⅰ)求證:PO平面![]() ;
;
(Ⅱ)求平面EFG與平面![]() 所成銳二面角的大小;
所成銳二面角的大小;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,若存在,求線段
,若存在,求線段![]() 的長度;若不存在,說明理由.
的長度;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電信運營公司為響應國家5G網絡建設政策,擬實行5G網絡流量階梯定價.每人月用流量中不超過![]() (一種流量計算單位)的部分按2元
(一種流量計算單位)的部分按2元![]() 收費;超出
收費;超出![]() 的部分按4元
的部分按4元![]() 收費.從用戶群中隨機調查了10000位用戶,獲得了他們某月的流量使用數據.整理得到如下的頻率分布直方圖:
收費.從用戶群中隨機調查了10000位用戶,獲得了他們某月的流量使用數據.整理得到如下的頻率分布直方圖:

(1)若![]() 為整數,依據本次調查,為使80
為整數,依據本次調查,為使80![]() 以上用戶在該月的流量價格為2元
以上用戶在該月的流量價格為2元![]() ,
,![]() 至少定為多少?
至少定為多少?
(2)假設同組中的每個數據用該組區間的右端點值代替,當![]() 時,試估計用戶該月的人均流量費.
時,試估計用戶該月的人均流量費.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知由n(n∈N*)個正整數構成的集合A={a1,a2,…,an}(a1<a2<…<an,n≥3),記SA=a1+a2+…+an,對于任意不大于SA的正整數m,均存在集合A的一個子集,使得該子集的所有元素之和等于m.
(1)求a1,a2的值;
(2)求證:“a1,a2,…,an成等差數列”的充要條件是“![]() ”;
”;
(3)若SA=2020,求n的最小值,并指出n取最小值時an的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
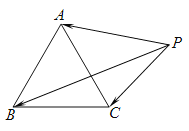
【題目】如圖,![]() 是邊長為1的正三角形,點P在
是邊長為1的正三角形,點P在![]() 所在的平面內,且
所在的平面內,且![]() (a為常數),下列結論中正確的是( )
(a為常數),下列結論中正確的是( )
A.當![]() 時,滿足條件的點P有且只有一個
時,滿足條件的點P有且只有一個
B.當![]() 時,滿足條件的點P有三個
時,滿足條件的點P有三個
C.當![]() 時,滿足條件的點P有無數個
時,滿足條件的點P有無數個
D.當a為任意正實數時,滿足條件的點總是有限個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電子設備工廠生產一種電子元件,質量控制工程師要在產品出廠前將次品檢出.估計這個廠生產的電子元件的次品率為0.2%,且電子元件是否為次品相互獨立,一般的檢測流程是:先把![]() 個
個![]() 電子元件串聯起來成組進行檢驗,若檢測通過,則全部為正品;若檢測不通過,則至少有一個次品,再逐一檢測,直到把所有的次品找出,若檢驗一個電子元件的花費為5分錢,檢驗一組(
電子元件串聯起來成組進行檢驗,若檢測通過,則全部為正品;若檢測不通過,則至少有一個次品,再逐一檢測,直到把所有的次品找出,若檢驗一個電子元件的花費為5分錢,檢驗一組(![]() 個)電子元件的花費為
個)電子元件的花費為![]() 分錢.
分錢.
(1)當![]() 時,估算一組待檢元件中有次品的概率;
時,估算一組待檢元件中有次品的概率;
(2)設每個電子元件檢測費用的期望為![]() ,求
,求![]() 的表達式;
的表達式;
(3)試估計![]() 的值,使每個電子元件的檢測費用的期望最小.(提示:用
的值,使每個電子元件的檢測費用的期望最小.(提示:用![]() 進行估算)
進行估算)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com