
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)討論函數![]() 的單調性;
的單調性;
(Ⅲ)對于任意![]() ,
,![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)分類討論,詳見解析;(Ⅲ)
;(Ⅱ)分類討論,詳見解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)當![]() 時,求出
時,求出![]() 可得切線的斜率,從而得到切線方程.
可得切線的斜率,從而得到切線方程.
(Ⅱ)求出![]() 后就
后就![]() 討論其符號后可得函數的單調區間.
討論其符號后可得函數的單調區間.
(Ⅲ)就![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分類討論后可得
分類討論后可得![]() 的最大值和最小值,從而得到關于
的最大值和最小值,從而得到關于![]() 的不等式組,其解即為所求的取值范圍.
的不等式組,其解即為所求的取值范圍.
解:(Ⅰ)當![]() 時,因為
時,因為![]()
所以![]() ,
,![]() .
.
又因為![]() ,
,
所以曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(Ⅱ)因為![]() ,
,
所以![]() .
.
令![]() ,解得
,解得![]() 或
或![]() .
.
若![]() ,當
,當![]() 即
即![]() 或
或![]() 時,
時,
故函數![]() 的單調遞增區間為
的單調遞增區間為![]() ;
;
當![]() 即
即![]() 時,故函數
時,故函數![]() 的單調遞減區間為
的單調遞減區間為![]() .
.
若![]() ,則
,則![]() ,
,
當且僅當![]() 時取等號,故函數
時取等號,故函數![]() 在
在![]() 上是增函數.
上是增函數.
若![]() ,當
,當![]() 即
即![]() 或
或![]() 時,
時,
故函數![]() 的單調遞增區間為
的單調遞增區間為![]() ;
;
當![]() 即
即![]() 時,故函數
時,故函數![]() 的單調遞減區間為
的單調遞減區間為![]() .
.
綜上,![]() 時,函數
時,函數![]() 單調遞增區間為
單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
![]() 時,函數
時,函數![]() 單調遞增區間為
單調遞增區間為![]() ;
;
![]() 時,函數
時,函數![]() 單調遞增區間為
單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() .
.
(Ⅲ) 由題設,只要![]() 即可.
即可.
令![]() ,解得
,解得![]() 或
或![]() .
.
當![]() 時,隨
時,隨![]() 變化,
變化,![]() 變化情況如下表:
變化情況如下表:
|
|
|
|
|
|
|
|
|
| ||
|
| 減 | 極小值 | 增 |
|
由表可知![]() ,此時
,此時![]() ,不符合題意.
,不符合題意.
當![]() 時,隨
時,隨![]() 變化,
變化,![]() 變化情況如下表:
變化情況如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
| 增 | 極大值 | 減 | 極小值 | 增 |
|
由表可得![]() ,
,
且![]() ,
,![]() ,
,
因![]() ,所以只需
,所以只需![]() ,
,
即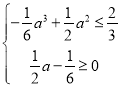 ,解得
,解得![]() .
.
當![]() 時,由(Ⅱ)知
時,由(Ⅱ)知![]() 在
在![]() 為增函數,
為增函數,
此時![]() ,符合題意.
,符合題意.
當![]() 時,
時,
同理只需![]() ,即
,即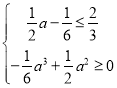 ,解得
,解得![]() .
.
當![]() 時,
時,![]() ,
,![]() ,不符合題意.
,不符合題意.
綜上,實數![]() 的取值范圍是
的取值范圍是![]() .
.


 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】一個調查學生記憶力的研究團隊從某中學隨機挑選100名學生進行記憶測試,通過講解100個陌生單詞后,相隔十分鐘進行聽寫測試,間隔時間![]() (分鐘)和答對人數
(分鐘)和答對人數![]() 的統計表格如下:
的統計表格如下:
時間 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
答對人數 | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
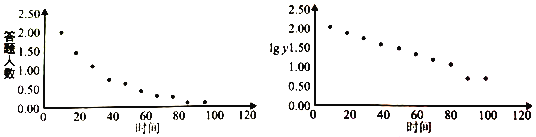
時間![]() 與答對人數
與答對人數![]() 的散點圖如圖:
的散點圖如圖:
附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,對于一組數據
,對于一組數據![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: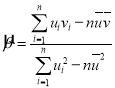 ,
,![]() .請根據表格數據回答下列問題:
.請根據表格數據回答下列問題:
(1)根據散點圖判斷,![]() 與
與![]() ,哪個更適宣作為線性回歸類型?(給出判斷即可,不必說明理由)
,哪個更適宣作為線性回歸類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果,建立![]() 與
與![]() 的回歸方程;(數據保留3位有效數字)
的回歸方程;(數據保留3位有效數字)
(3)根據(2)請估算要想記住![]() 的內容,至多間隔多少分鐘重新記憶一遍.(參考數據:
的內容,至多間隔多少分鐘重新記憶一遍.(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4-4:坐標系與參數方程)
在直角坐標系![]() 中,半圓C的參數方程為
中,半圓C的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),以O為極點,x軸的非負半軸為極軸建立極坐標系.
),以O為極點,x軸的非負半軸為極軸建立極坐標系.
(Ⅰ)求C的極坐標方程;
(Ⅱ)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線OM:
,射線OM:![]() 與半圓C的交點為O、P,與直線
與半圓C的交點為O、P,與直線![]() 的交點為Q,求線段PQ的長.
的交點為Q,求線段PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班主任對全班50名學生學習積極性和對待班級工作的態度進行了調查,統計數據如下表所示:
積極參加 班級工作 | 不太主動參加 班級工作 | 合計 | |
學習積極性高 | 18 | 7 | 25 |
學習積極性一般 | 6 | 19 | 25 |
合計 | 24 | 26 | 50 |
(1)如果隨機抽查這個班的一名學生,那么抽到積極參加班級工作的學生的概率是多少?抽到不太主動參加班級工作且學習積極性一般的學生的概率是多少?
(2)試運用獨立性檢驗的思想方法能否有99.9%的把握認為學生的學習積極性與對待班級工作的態度有關系?并說明理由.(參考下表)
P(K2 ≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式: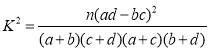 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在“挑戰不可能”的電視節目上,甲、乙、丙三個人組成的解密團隊參加一項解密挑戰活動,規則是由密碼專家給出題目,然后由![]() 個人依次出場解密,每人限定時間是
個人依次出場解密,每人限定時間是![]() 分鐘內,否則派下一個人.
分鐘內,否則派下一個人.![]() 個人中只要有一人解密正確,則認為該團隊挑戰成功,否則挑戰失敗.根據甲以往解密測試情況,抽取了甲
個人中只要有一人解密正確,則認為該團隊挑戰成功,否則挑戰失敗.根據甲以往解密測試情況,抽取了甲![]() 次的測試記錄,繪制了如下的頻率分布直方圖.
次的測試記錄,繪制了如下的頻率分布直方圖.
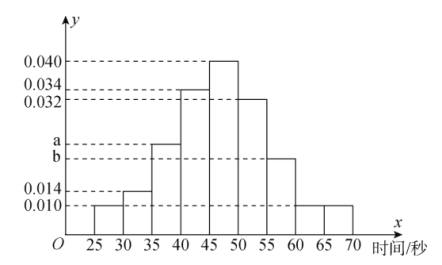
(1)若甲解密成功所需時間的中位數為![]() ,求
,求![]() 、
、![]() 的值,并求出甲在
的值,并求出甲在![]() 分鐘內解密成功的頻率;
分鐘內解密成功的頻率;
(2)在“挑戰不可能”節目上由于來自各方及自身的心理壓力,甲,乙,丙解密成功的概率分別為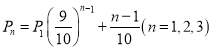 ,其中
,其中![]() 表示第
表示第![]() 個出場選手解密成功的概率,并且
個出場選手解密成功的概率,并且![]() 定義為甲抽樣中解密成功的頻率代替,各人是否解密成功相互獨立.
定義為甲抽樣中解密成功的頻率代替,各人是否解密成功相互獨立.
①求該團隊挑戰成功的概率;
②該團隊以![]() 從小到大的順序按排甲、乙、丙三個人上場解密,求團隊挑戰成功所需派出的人員數目
從小到大的順序按排甲、乙、丙三個人上場解密,求團隊挑戰成功所需派出的人員數目![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 的最大值為
的最大值為![]() .
.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(Ⅲ)當![]() 時,令
時,令![]() ,是否存在區間
,是否存在區間![]() .使得函數
.使得函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() 若存在,求實數
若存在,求實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的檢驗員為了檢測生產線上生產零件的情況,從產品中隨機抽取了![]() 個進行測量,根據所測量的數據畫出頻率分布直方圖如下:
個進行測量,根據所測量的數據畫出頻率分布直方圖如下:

如果:尺寸數據在![]() 內的零件為合格品,頻率作為概率.
內的零件為合格品,頻率作為概率.
(1)從產品中隨機抽取![]() 件,合格品的個數為
件,合格品的個數為![]() ,求
,求![]() 的分布列與期望:
的分布列與期望:
(2)為了提高產品合格率,現提出![]() ,
,![]() 兩種不同的改進方案進行試驗,若按
兩種不同的改進方案進行試驗,若按![]() 方案進行試驗后,隨機抽取
方案進行試驗后,隨機抽取![]() 件產品,不合格個數的期望是
件產品,不合格個數的期望是![]() :若按
:若按![]() 方案試驗后,抽取
方案試驗后,抽取![]() 件產品,不合格個數的期望是
件產品,不合格個數的期望是![]() ,你會選擇哪個改進方案?
,你會選擇哪個改進方案?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自2017年7月27日上映以來,《戰狼2》的票房一路高歌猛進,并不斷刷新華語電影票房紀錄.繼8月25日官方宣布沖破53億票房之后,根據外媒Worldwide Box Office給出的2017年周末全球票房最新排名,《戰狼2》以8.151億美元(約54.18億元)的成績成功殺入前五.通過收集并整理了《戰狼2》上映前兩周的票房(單位:億元)數據,繪制出下面的條形圖.根據該條形圖,下列結論錯誤的是( )
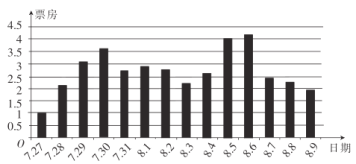
A.在《戰狼2》上映前兩周中,前四天票房逐日遞增
B.在《戰狼2》上映前兩周中,日票房超過2億元的共有12天
C.在《戰狼2》上映前兩周中,8月5日,8月6日達到了票房的高峰期
D.在《戰狼2》上映前兩周中,前五日的票房平均數高于后五日的票房平均數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為建設美麗新農村,某村對本村布局重新進行了規劃,其平面規劃圖如圖所示,其中平行四邊形![]() 區域為生活區,
區域為生活區,![]() 為橫穿村莊的一條道路,
為橫穿村莊的一條道路,![]() 區域為休閑公園,
區域為休閑公園,![]() ,
,![]() ,
,![]() 的外接圓直徑為
的外接圓直徑為![]() .
.

(1)求道路![]() 的長;
的長;
(2)該村準備沿休閑公園的邊界修建柵欄,以防村中的家畜破壞公園中的綠化,試求柵欄總長的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com