
【題目】已知等比數列{![]() }的前n項和為
}的前n項和為![]() ,且滿足2
,且滿足2![]() =
=![]() +m(m∈R).
+m(m∈R).
(Ⅰ)求數列{![]() }的通項公式;
}的通項公式;
(Ⅱ)若數列{![]() }滿足
}滿足![]() ,求數列{
,求數列{![]() }的前n項和
}的前n項和![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)法一:由前n項和與數列通項公式的關系可得數列的通項公式為![]() ;
;
法二:由題意可得 ,則
,則![]() ,據此可得數列的通項公式為
,據此可得數列的通項公式為![]() .
.
(Ⅱ)由(Ⅰ)可得![]() ,裂項求和可得
,裂項求和可得![]() .
.
(Ⅰ)法一:
由![]() 得
得![]() ,
,
當![]() 時,
時,![]() ,即
,即![]() ,
,
又![]() ,當
,當![]() 時符合上式,所以通項公式為
時符合上式,所以通項公式為![]() .
.
法二:
由![]() 得
得
從而有![]() ,
,
所以等比數列公比![]() ,首項
,首項![]() ,因此通項公式為
,因此通項公式為![]() .
.
(Ⅱ)由(Ⅰ)可得![]() ,
,
![]() ,
,
![]() .
.
【點睛】
本題主要考查數列前n項和與通項公式的關系,裂項求和的方法等知識,意在考查學生的轉化能力和計算求解能力.
【題型】解答題
【結束】
18
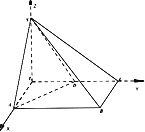
【題目】四棱錐S-ABCD的底面ABCD為直角梯形,AB∥CD,AB⊥BC,AB=2BC=2CD=2,△SAD為正三角形.
(Ⅰ)點M為棱AB上一點,若BC∥平面SDM,AM=λAB,求實數λ的值;
(Ⅱ)若BC⊥SD,求二面角A-SB-C的余弦值.

【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)由線面平行的性質定理可得![]() ,據此可知四邊形BCDM為平行四邊形,據此可得
,據此可知四邊形BCDM為平行四邊形,據此可得![]() .
.
(Ⅱ)由幾何關系,在平面![]() 內過點
內過點![]() 作
作![]() 直線
直線![]() 于點
于點![]() ,以點E為坐標原點,EA方向為X軸,EC方向為Y軸,ES方向為Z軸建立空間坐標系,據此可得平面
,以點E為坐標原點,EA方向為X軸,EC方向為Y軸,ES方向為Z軸建立空間坐標系,據此可得平面![]() 的一個法向量
的一個法向量![]() ,平面
,平面![]() 的一個法向量
的一個法向量![]() ,據此計算可得二面角
,據此計算可得二面角![]() 余弦值為
余弦值為![]() .
.
(Ⅰ)因為![]() 平面SDM,
平面SDM,![]()
![]() 平面ABCD,平面SDM
平面ABCD,平面SDM ![]() 平面ABCD=DM,所以
平面ABCD=DM,所以![]() ,
,
因為![]() ,所以四邊形BCDM為平行四邊形,又
,所以四邊形BCDM為平行四邊形,又![]() ,所以M為AB的中點.
,所以M為AB的中點.
因為![]()
![]() .
.
(Ⅱ)因為![]()
![]() ,
, ![]()
![]() ,所以
,所以![]() 平面
平面![]() ,又因為
,又因為![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
在平面![]() 內過點
內過點![]() 作
作![]() 直線
直線![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() ,
,
在![]() 和
和![]() 中,因為
中,因為![]() ,所以
,所以![]() ,
,
又由題知![]() ,所以
,所以![]() 所以
所以![]() ,
,
以下建系求解.以點E為坐標原點,EA方向為X軸,EC方向為Y軸,ES方向為Z軸建立如圖所示空間坐標系,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,則
,則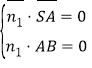 ,所
,所![]() ,
,
令![]() 得
得![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
同理得![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
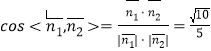 ,因為二面角
,因為二面角![]() 為鈍角.
為鈍角.
所以二面角![]() 余弦值為
余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C的對邊分別為a,b,c且面積為S,滿足S= ![]() bccosA
bccosA
(1)求cosA的值;
(2)若a+c=10,C=2A,求b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設xOy,![]() 為兩個平面直角坐標系,它們具有相同的原點,Ox正方向到
為兩個平面直角坐標系,它們具有相同的原點,Ox正方向到![]() 正方向的角度為θ,那么對于任意的點M,在xOy下的坐標為(x,y),那么它在
正方向的角度為θ,那么對于任意的點M,在xOy下的坐標為(x,y),那么它在![]() 坐標系下的坐標(
坐標系下的坐標(![]() ,
,![]() )可以表示為:
)可以表示為:![]() =xcosθ+ysinθ,
=xcosθ+ysinθ,![]() =ycosθ-xsinθ.根據以上知識求得橢圓3
=ycosθ-xsinθ.根據以上知識求得橢圓3![]() -
-![]() +
+![]() -1=0的離心率為
-1=0的離心率為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大提出,加快水污染防治,建設美麗中國.根據環保部門對某河流的每年污水排放量![]() (單位:噸)的歷史統計數據,得到如下頻率分布表:
(單位:噸)的歷史統計數據,得到如下頻率分布表:

將污水排放量落入各組的頻率作為概率,并假設每年該河流的污水排放量相互獨立.
(1)求在未來3年里,至多1年污水排放量![]() 的概率;(2)該河流的污水排放對沿河的經濟影響如下:當
的概率;(2)該河流的污水排放對沿河的經濟影響如下:當![]() 時,沒有影響;當
時,沒有影響;當![]() 時,經濟損失為10萬元;當
時,經濟損失為10萬元;當![]() 時,經濟損失為60萬元.為減少損失,現有三種應對方案:
時,經濟損失為60萬元.為減少損失,現有三種應對方案:
方案一:防治350噸的污水排放,每年需要防治費3.8萬元;
方案二:防治310噸的污水排放,每年需要防治費2萬元;
方案三:不采取措施.
試比較上述三種文案,哪種方案好,并請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)當a=2時,求不等式f(x)<g(x)的解集;
(2)設a> ![]() ,且當x∈[
,且當x∈[ ![]() ,a]時,f(x)≤g(x),求a的取值范圍.
,a]時,f(x)≤g(x),求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com