
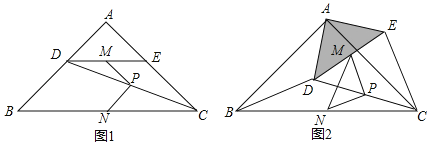
【題目】如圖1,在Rt△ABC中,∠A=90°,AB=AC,點D,E分別在邊AB,AC上,AD=AE,連接DC,點M,P,N分別為DE,DC,BC的中點.
(1)觀察猜想:圖1中,線段PM與PN的數(shù)量關系是 ,位置關系是 ;
(2)探究證明:把△ADE繞點A逆時針方向旋轉到圖2的位置,連接MN,BD,CE,判斷△PMN的形狀,并說明理由;
(3)拓展延伸:把△ADE繞點A在平面內自由旋轉,若AD=4,AB=10,請直接寫出△PMN面積的最大值.
【答案】(1)PM=PN,PM⊥PN;(2)△PMN是等腰直角三角形,證明詳見解析;(3)![]() .
.
【解析】
(1)利用三角形的中位線得出PM=![]() CE,PN=
CE,PN=![]() BD,進而判斷出BD=CE,即可得出結論,再利用三角形的中位線得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出結論;
BD,進而判斷出BD=CE,即可得出結論,再利用三角形的中位線得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出結論;
(2)先判斷出△ABD≌△ACE,得出BD=CE,同(1)的方法得出PM=![]() BD,PN=
BD,PN=![]() BD,即可得出PM=PN,同(1)的方法即可得出結論;
BD,即可得出PM=PN,同(1)的方法即可得出結論;
(3)方法1、先判斷出MN最大時,△PMN的面積最大,進而求出AN,AM,即可得出MN最大=AM+AN,最后用面積公式即可得出結論.
方法2、先判斷出BD最大時,△PMN的面積最大,而BD最大是AB+AD=14,即可.
解:(1)∵點P,N是BC,CD的中點,
∴PN∥BD,PN=![]() BD,
BD,
∵點P,M是CD,DE的中點,
∴PM∥CE,PM=![]() CE,
CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案為:PM=PN,PM⊥PN;
(2)△PMN是等腰直角三角形.
由旋轉知,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,BD=CE,
利用三角形的中位線得,PN=![]() BD,PM=
BD,PM=![]() CE,
CE,
∴PM=PN,
∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE,
∴∠DPM=∠DCE,
同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
∴△PMN是等腰直角三角形;
(3)方法1:如圖2,
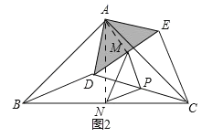
同(2)的方法得,△PMN是等腰直角三角形,
∴MN最大時,△PMN的面積最大,
∴DE∥BC且DE在頂點A上面,
∴MN最大=AM+AN,
連接AM,AN,
在△ADE中,AD=AE=4,∠DAE=90°,
∴AM=![]() ,
,
在Rt△ABC中,AB=AC=10,AN=![]() ,
,
∴MN最大=![]() ,
,
∴S△PMN最大=![]() PM2=
PM2=![]() ×
×![]() MN2=
MN2=![]() ×(
×(![]() )2=
)2=![]() ;
;
方法2:由(2)知,△PMN是等腰直角三角形,PM=PN=![]() BD,
BD,
∴PM最大時,△PMN面積最大,
∴點D在BA的延長線上,
∴BD=AB+AD=14,
∴PM=7,
∴S△PMN最大=![]() PM2=
PM2=![]() ×72=
×72=![]() .
.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:初中數(shù)學 來源: 題型:
【題目】中學生上學帶手機的現(xiàn)象越來越受到社會的關注,為此媒體記者隨機調查了某校若干名學生上學帶手機的目的,分為四種類型:A接聽電話;B收發(fā)短信;C查閱資料;D游戲聊天.并將調查結果繪制成圖1和圖2的統(tǒng)計圖(不完整),請根據(jù)圖中提供的信息,解答下列問題:
(1)此次抽樣調查中,共調查了 名學生;
(2)將圖1、圖2補充完整;
(3)現(xiàn)有4名學生,其中A類兩名,B類兩名,從中任選2名學生,求這兩名學生為同一類型的概率(用列表法或樹狀圖法).

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
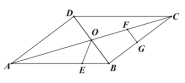
【題目】在平行四邊形![]() 中,對角線
中,對角線![]() 、
、![]() 交于點
交于點![]() ,
,![]() ,
,![]() ,
,![]() 點
點![]() 從點
從點![]() 出發(fā),沿
出發(fā),沿![]() 方向勻速運動,速度為
方向勻速運動,速度為![]() ;同時,點
;同時,點![]() 從點
從點![]() 出發(fā),沿
出發(fā),沿![]() 方向勻速運動,速度為
方向勻速運動,速度為![]() ;當一個點停止運動時,另一個點也停止運動.連接
;當一個點停止運動時,另一個點也停止運動.連接![]() ,過點
,過點![]() 作
作![]() ,設運動時間為
,設運動時間為![]() ,
,
解答下列問題:
(1)當![]() 為何值時
為何值時![]() 是等腰三角形?
是等腰三角形?
(2)設五邊形![]() 面積為
面積為![]() ,試確定
,試確定![]() 與
與![]() 的函數(shù)關系式;
的函數(shù)關系式;
(3)在運動過程中,是否存在某一時刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(4)在運動過程中,是否存在某一時刻![]() 使得
使得![]() 平分
平分![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
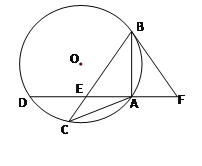
【題目】如圖,△ABC內接于⊙O,且AB=AC,點D在⊙O上,AD⊥AB于點A, AD與 BC交于點E,F在DA的延長線上,且AF=AE.
(1)求證:BF是⊙O的切線;
(2)若AD=4,![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
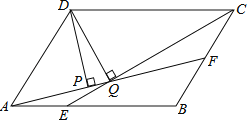
【題目】如圖,平行四邊形ABCD中,AB=3,BC=2,∠DAB=60°,E在AB上,且AE=![]() EB,F是BC的中點,過D分別作DP⊥AF于P,DQ⊥CE于Q,則DP:DQ的值為_____.
EB,F是BC的中點,過D分別作DP⊥AF于P,DQ⊥CE于Q,則DP:DQ的值為_____.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
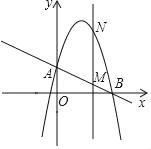
【題目】如圖,已知拋物線y=﹣x2+bx+c(b,c是常數(shù))經過A(0,2)、B(4,0)兩點.
(1)求該拋物線的解析式和頂點坐標;
(2)作垂直x軸的直線x=t,在第一象限交直線AB于M,交這條拋物線于N,求當t取何值時,MN有最大值?最大值是多少?
(3)在(1)的情況下,以A、M、N、D為頂點作平行四邊形,請直接寫出第四個頂點D的所有坐標(直接寫出結果,不必寫解答過程)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】紅旗連鎖超市準備購進甲、乙兩種綠色袋裝食品.甲、乙兩種綠色袋裝食品的進價和售價如表.已知:用2000元購進甲種袋裝食品的數(shù)量與用1600元購進乙種袋裝食品的數(shù)量相同.
甲 | 乙 | |
進價(元/袋) |
|
|
售價(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使購進的甲、乙兩種綠色袋裝食品共800袋的總利潤(利潤=售價-進價)不少于4800元,且不超過4900元,問該超市有幾種進貨方案?
(3)在(2)的條件下,該超市如果對甲種袋裝食品每袋優(yōu)惠![]() 元出售,乙種袋裝食品價格不變.那么該超市要獲得最大利潤應如何進貨?
元出售,乙種袋裝食品價格不變.那么該超市要獲得最大利潤應如何進貨?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,二次函數(shù)![]() 的圖象交
的圖象交![]() 軸于
軸于![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,點
,點![]() 的坐標為
的坐標為![]() ,頂點
,頂點![]() 的坐標為
的坐標為![]() .
.

(1)求二次函數(shù)的解析式和直線![]() 的解析式;
的解析式;
(2)點![]() 是直線
是直線![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 軸的垂線,交拋物線于點
軸的垂線,交拋物線于點![]() ,當點
,當點![]() 在第一象限時,求線段
在第一象限時,求線段![]() 長度的最大值;
長度的最大值;
(3)在拋物線上是否存在異于![]() 的點
的點![]() ,使
,使![]() 中
中![]() 邊上的高為
邊上的高為![]() ,若存在求出點
,若存在求出點![]() 的坐標;若不存在請說明理由.
的坐標;若不存在請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
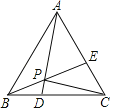
【題目】如圖所示,等邊△ABC的邊長為4,點D是BC邊上一動點,且CE=BD,連接AD,BE,AD與BE相交于點P,連接PC.則線段PC的最小值等于_____.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com